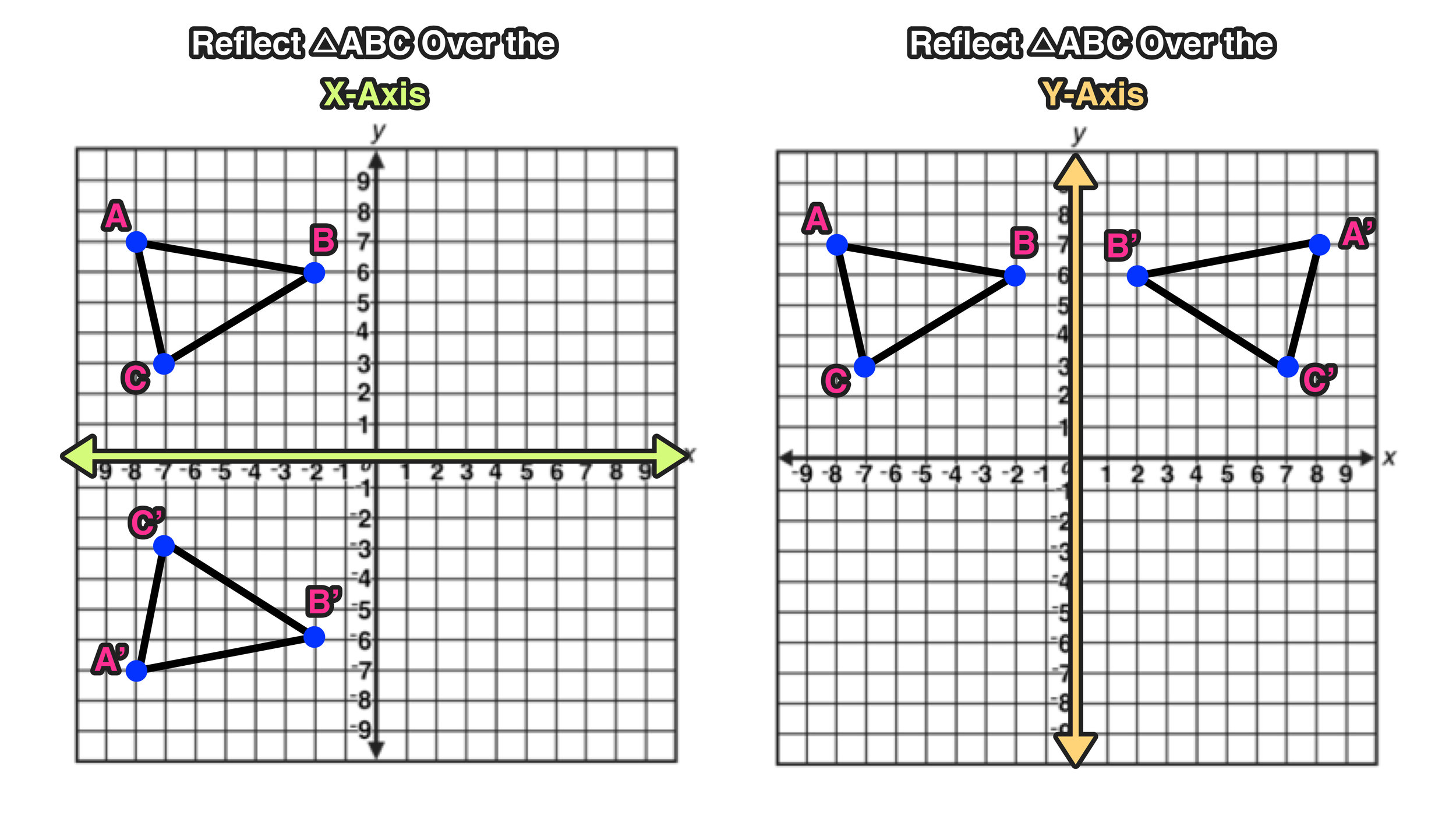
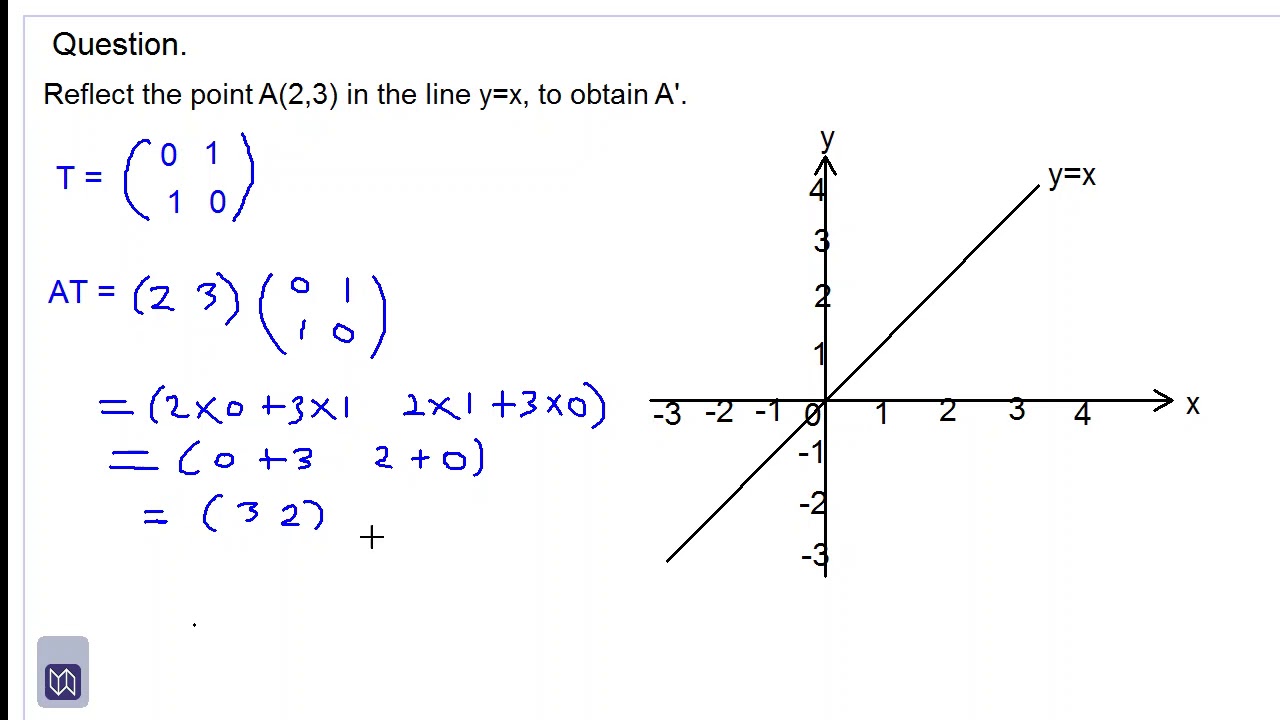
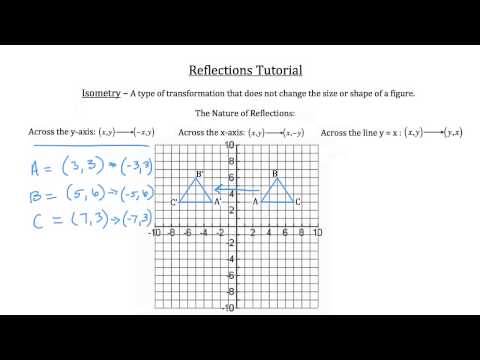
When a point is reflected over y=x, the following change occurs ⇒ We are given the point (7,8) Essentially, we change the signs for both coordinates, then flip the xcoordinate and ycoordinate 1 Change the signs ⇒ 2 Flip the x and y coordinatesOne final common reflection we see a lot is the reflection of a figure over the line y = x Let's examine a different figure in order to see the effects of this reflection To the right we have triangle PQR with points (1, 1), (4, 1), and (1, 3), respectively10/5/19 · A reflection of a point, a line, or a figure in the X axis involved reflecting the image over the x axis to create a mirror image In this case, the x axis would be called the axis of reflection Math Definition Reflection Over the Y Axis A reflection of a point, a line, or a figure in the Y axis involved reflecting the image over the Y axis to create a mirror image

Transformations
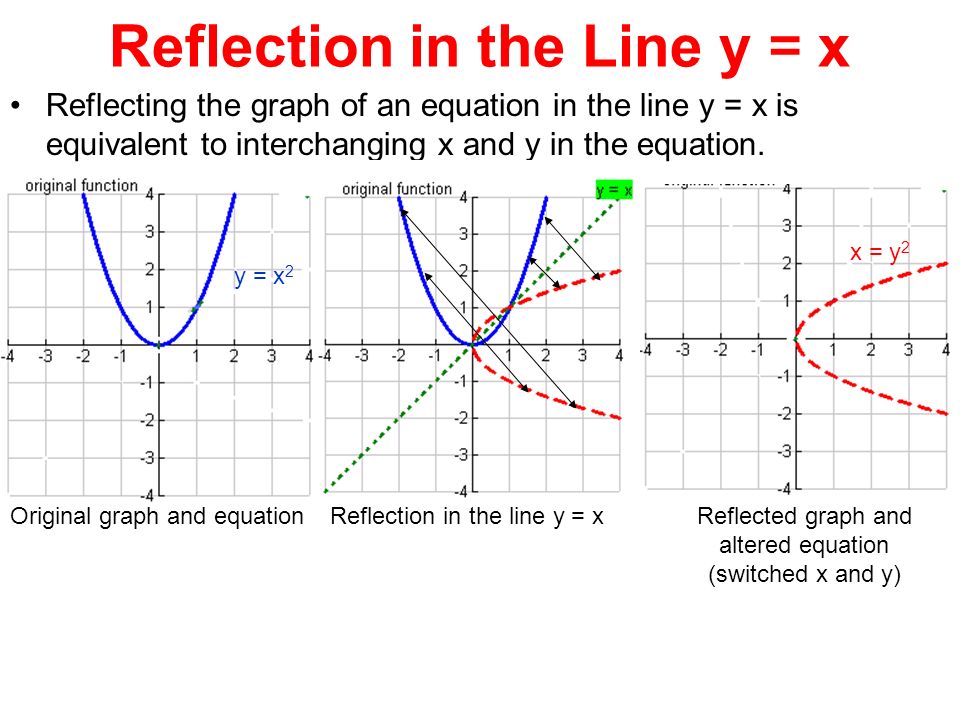
Reflection over the line y=x
Reflection over the line y=x-Reflect over the y = x When you reflect a point across the line y = x, the x coordinate and y coordinate change places If you reflect over the line y = x, the x coordinate and y coordinate change places and are negated (the signs are changed) The reflection of the point (x,y) acrossWhat is a Reflection?


Reflection Over The X And Y Axis The Complete Guide Mashup Math
· so the image point is 4 units from the line of reflection ie x' = 2 4 = 6 ∴ (− 2, − 5) → (6, −5)26/9/19 · SHOW ANSWER C, the line y = x The formula for reflecting across the line y = x is (x, y) > (y, x) If the original coordinates are (12, 7), and they become (7, 12), the x and y values have swapped places, showing a reflection over the line y = x Thanks21/2/11 · we've talked a lot about linear transformations what I want to do in this video and actually the next few videos is to show you how to essentially design linear transformations to do things to vectors that you want them to do so we already know that if I have some linear transformation T and it's a mapping from RN to R M that we can represent T what T does to any
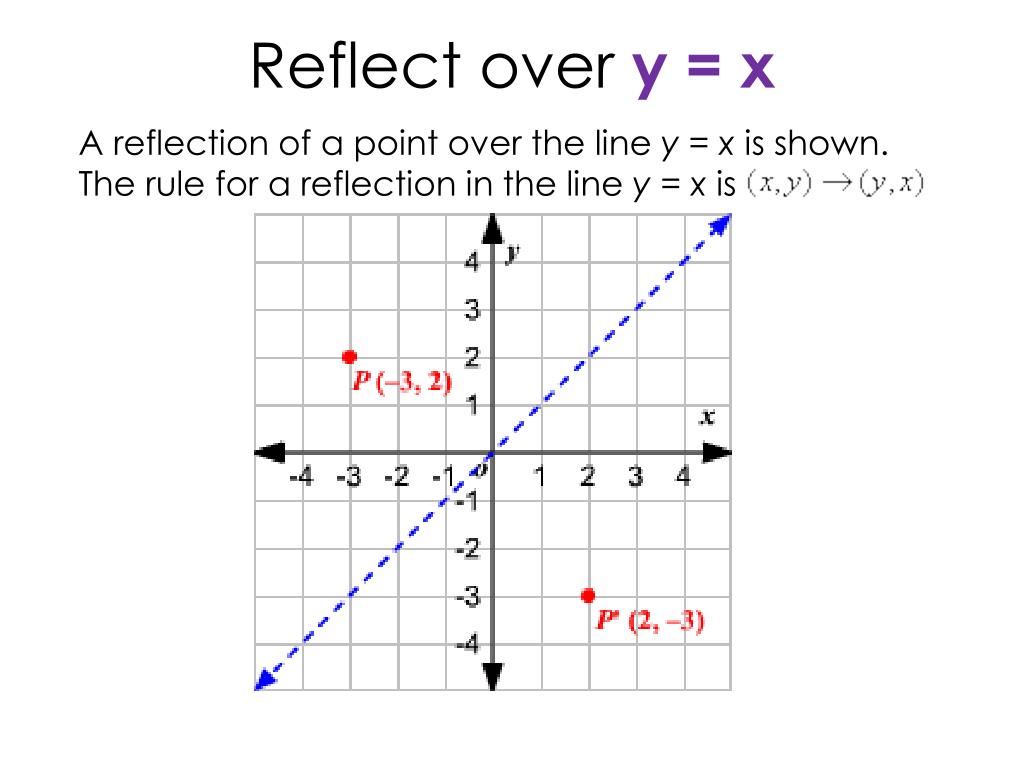
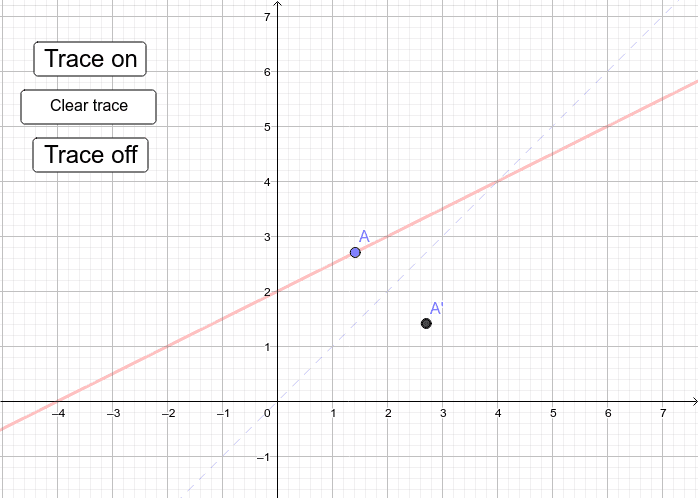
1/11/13 · How to reflect a point over the y=x axis How to reflect a point over the y=x axis Watch later Share Copy link Info Shopping Tap19/6/ · A Condition of Reflection when Y = X Take the case where a point is reflecting across a line Y=X Now, the X and Y coordinates will interchange their positions However, the signs get negated/cancelled when the point of reflection takes place over a line Y = X, but the point of coordinates still changes places (Image to be added soon)A reflection in the line y = x can be seen in the picture below in which A is reflected to its image A' The general rule for a reflection in the y = x (A, B) → (B, A)
4 Reflection about line y=x The object may be reflected about line y = x with the help of following transformation matrix First of all, the object is rotated at 45° The direction of rotation is clockwise After it reflection is done concerning xaxis The last step is the rotation of y=x back to its original position that is · Reflection over Y = X When a point is reflected across the line y = x, the xcoordinates and ycoordinates change their place Similarly, when a point is reflected across the line y = x, the xcoordinates and ycoordinates change their place and are negatedThis lesson is presented by Glyn CaddellFor more lessons, quizzes and practice tests visit http//caddellpreponlinecomFollow Glyn on twitter http//twitter


What Is The Reflection Image Of 5 3 In The Line Y X Socratic


Ppt Reflect Over Y X Powerpoint Presentation Free Download Id
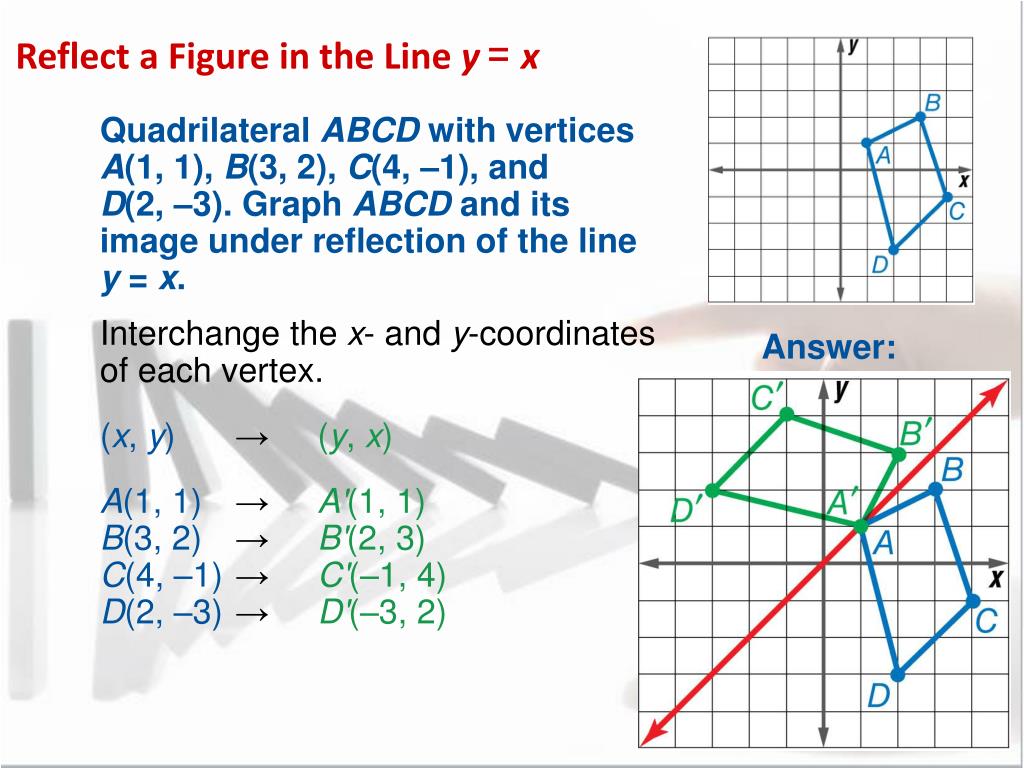
To reflect points across the line y = −x y = − x, we must swap the coordinates and change their signs To see why this works, consider the first and third quadrants Reflecting the first quadrantThe fixed line is called the line of reflection A reflection of a point over the line y = − x y = −x is shown The rule for a reflection in the origin is (x, y) → (− y, − x) Explanation It's astonishing how difficult it is to find a good explanation how to reflect a point over a lineReflection about the line y = x Once students understand the rules which they have to apply for reflection transformation, they can easily make reflection transformation of a figure Let us consider the following example to have better understanding of reflection



How Are We Studying Transformations Differently By Eureka Math Eureka Math Medium



Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor
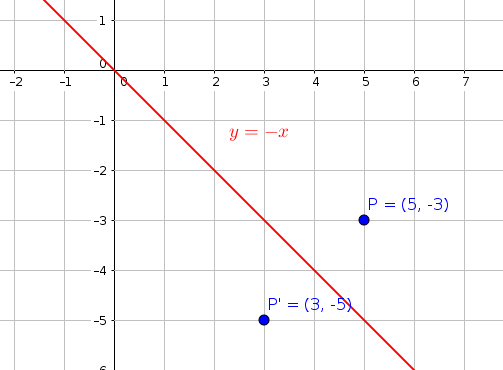
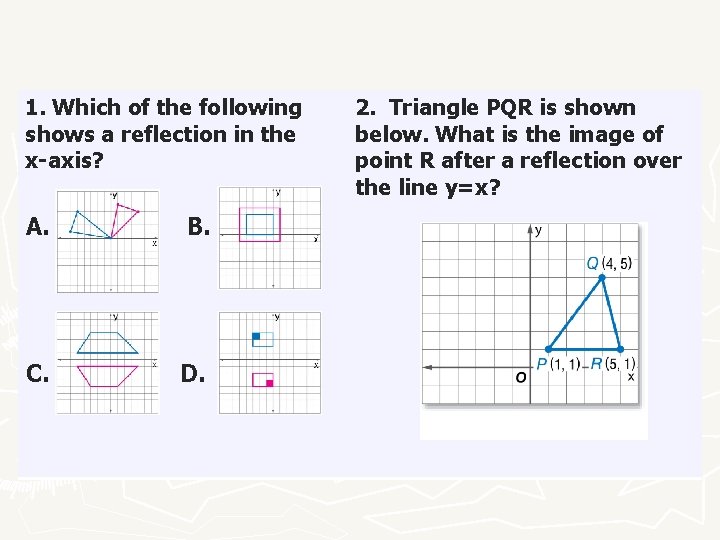
11/6/19 · Click here 👆 to get an answer to your question ️ Trapezoid ABCD is reflected over the line y = x What rule shows the input and output of the reflection, andSubmit Answer 1 See answer woodtoogood is waiting for your help Add your answer and earn points laurynmayfield1213 laurynmayfield1213 Answer (8,0) Stepbystep explanation New questions in Mathematics 6Reflecting a point over a line It's astonishing how difficult it is to find a good explanation how to reflect a point over a line that does not use higher math methods So here is my explanation You have a point P = ( x, y) and a line g ( x) = m ⋅ x t and you want to get the point



Reflections


Ppt 9 1 Reflections Powerpoint Presentation Free Download Id
The linear transformation rule (p, s) → (r, s) for reflecting a figure over the oblique line y = mx b where r and s are functions of p, q, b, and θ = Tan 1 (m) is shown below Finding the linear transformation rule given the equation of the line of reflection equation y = mx b involves using a calculator to find angle θ = Tan 1 (mReflection over y=x Reflection over y=x Share Video https//wwwshowmecom/sh/?h=d5WHhqa Share Video 0000Use our online point reflection calculator to know the point reflection for the given coordinates This calculator helps you to find the point reflection A, for the given coordinates of A(x,y) Just select an axis from the dropdown and enter the coordinates, the point reflection calculator will show the result


Section 4 3 Reflecting Graphs Symmetry Objective To Reflect Graphs And To Use Symmetry To Sketch Graphs Ppt Download



Holt Geometry Ch 12 Flashcards Quizlet
The transformation is done over a line of reflection it flips a plane about a fixed line An isometry is a transformation that preserves distance The parallelogram is reflected across the line y = x Which of the following are coordinates of a vertex of the image?A) A reflection across the line y = x B) A reflection across the line y = 2x C) A rotation of 180 degrees clockwise about the origin D) A reflection across the xaxis, and then a reflection across the yaxis E) A rotation of 270 degrees counterclockwise about the origin, and then a reflection across the xaxis 4Graph the line Ask students to start with point A and reflect it over the line My students told me to go left 2 squares to get to y = xx and then 2 more squares past that to create the new line While this is the method we learned for reflecting points over a line, we always had a horizontal or vertical line, not a diagonal line
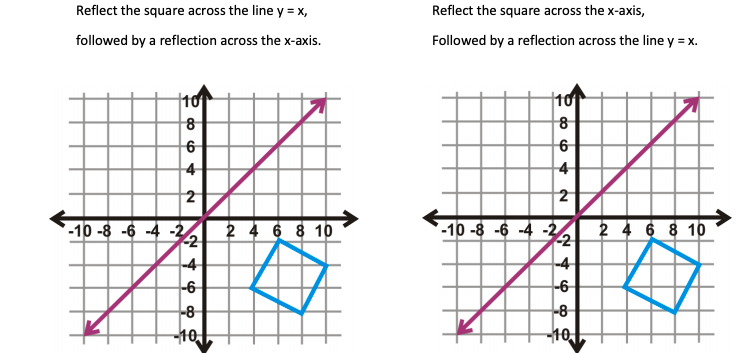


Solved Reflect The Square Across The Line Y X Followed Chegg Com



Reflection In The Line Y X Transformation Matrix Youtube
Play this game to review Geometry B(2, 4) Reflect over the line y = x14 Reflections Over y = x, y = –x, y = #, & x = # Geometry Directions Write the rule of the transformation (This is a mixed review) 1) A line segment is reflected over y = –x 2) A line segment is translated 5 units left & 1 unit up22/1/16 · Active Oldest Votes 1 To reflect over a vertical line, such as x = a, first translate so the line is shifted to the yaxis, then reflect over it, then translate back so the line is shifted to its original position ( x, y) ↦ ( x − a, y) ↦ ( a − x, y) ↦ ( 2 a − x, y) In this case to reflex over x = − 1 we shift x ↦ x 1



How To Find A Reflection Image


Reflecting In The Line Y X 2 Geogebra
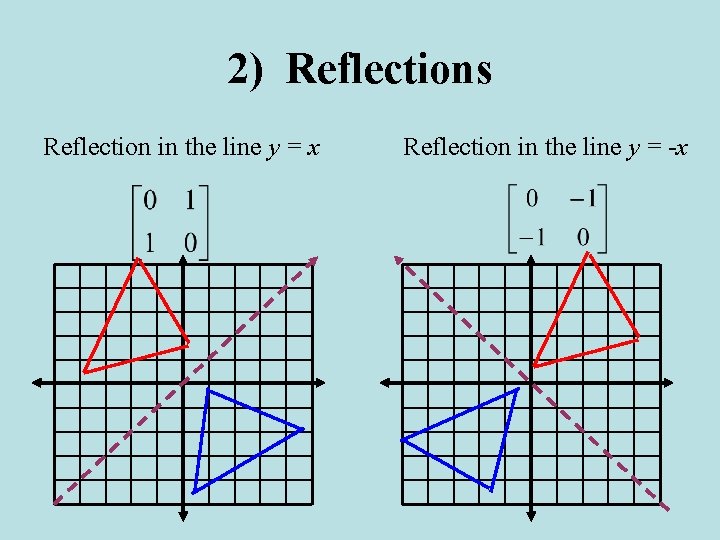
On this lesson, you will learn how to perform reflections over the xaxis and reflections over the yaxis (also known as across the xaxis and across the yaWolframAlpha Widgets "Reflection Calculator MyALevelMathsTutor" Free Education Widget Get the free "Reflection Calculator MyALevelMathsTutor" widget for your website, blog, Wordpress, Blogger, or iGoogle Find more Education widgets in WolframAlpha HOMEABOUTPRODUCTSBUSINESSRESOURCESA shape can be reflected in the line y = −x If point on a shape is reflected in the line y = −x both coordinates change sign (the coordinate becomes negative if it is positive and vice versa) the xcoordinate becomes the ycoordinate and the ycoordinate becomes the xcoordinate



Reflection
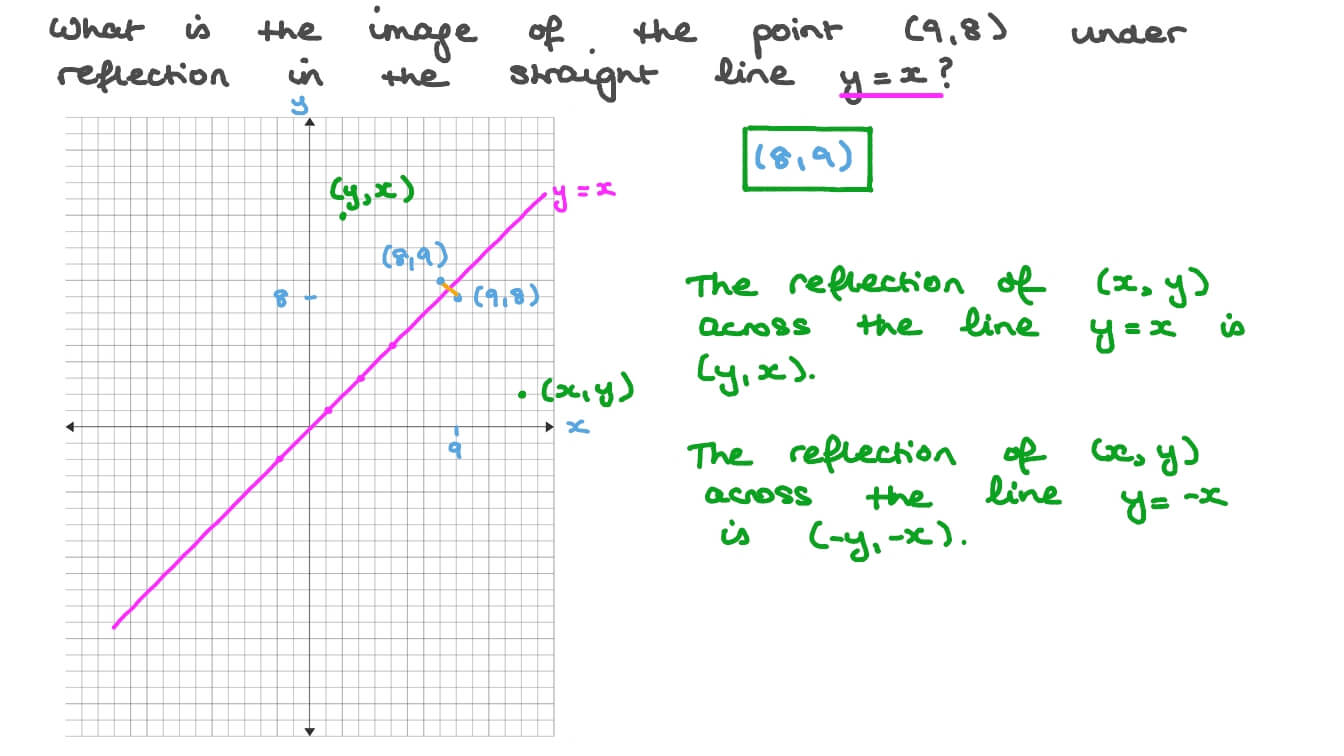


Question Video Determining The Position Of A Point After Reflecting In A Given Straight Line Given The Point S Coordinates Nagwa
Reflection about the line y=x Once students understand the rules which they have to apply for reflection transformation, they can easily make reflection transformation of a figure For example, if we are going to make reflection transformation of the point (2,3) about xaxis, after transformation, the point would be (2,3)I'm struggling to reflect curves over the line of $ y = x $, I have no trouble reflecting shapes over the x or y axis, but always struggle when it comes to $ y = x$ I always have to resort to plotting which takes up a lot of timeWhen you look in the mirror, you see your reflection In math, you can create mirror images of figures by reflecting them over a given line This tutorial introduces you to reflections and shows you some examples of reflections Take a look!


Math Alive Geometry 1
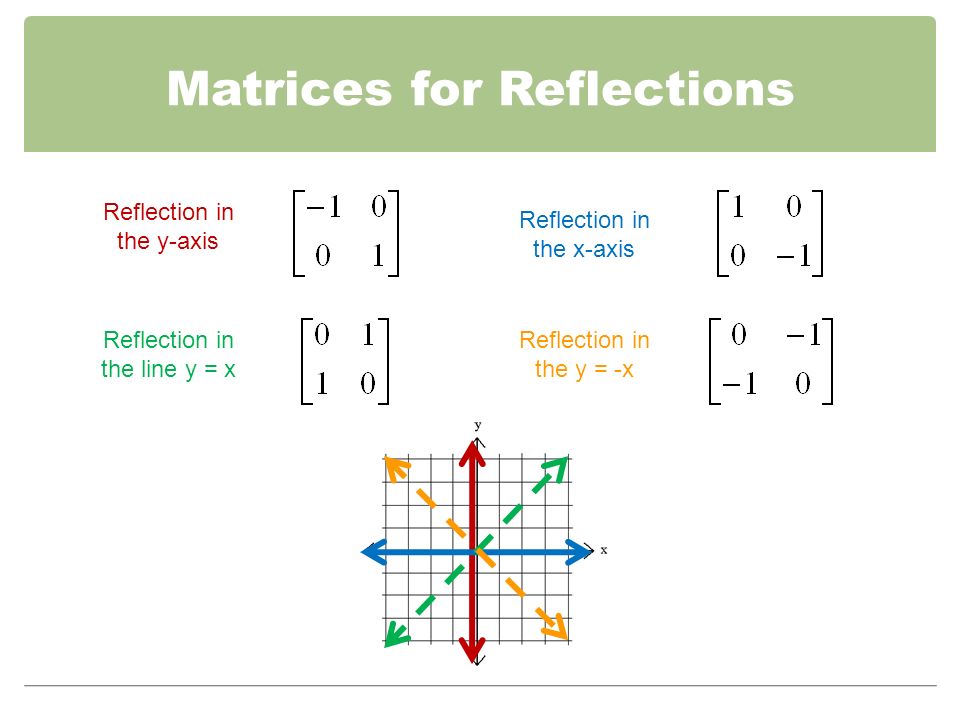


4 4 Geometric Transformations With Matrices Objectives To Represent Translations And Dilations W Matrices To Represent Reflections And Rotations With Ppt Download
How to reflect a triangle over the y=x line How to reflect a triangle over the y=x line Watch later Share Copy link Info Shopping Tap to unmute If playback doesn't begin shortlyTap to unmute If playback doesn't begin shortly, try restarting your device Up Next Transformation Reflection (across y = x) FerranteMath Cancel Autoplay is paused Transformation ReflectionA graph can be reflected in three ways across the axes, the origin and the line y = x There are specific rules to perform each reflection This lesson will describe those rules and show you how



Reflection Transformation
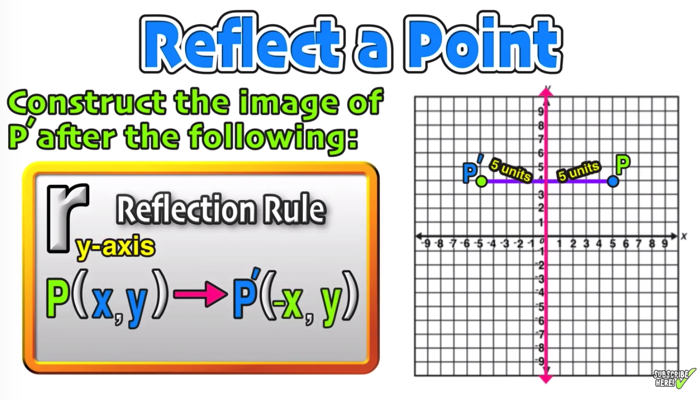


Reflection Over The X And Y Axis The Complete Guide Mashup Math
The rule for a reflection over the y axis is ( x , y ) → ( − x , y ) Reflection in the line y = x A reflection of a point over the line y = x is shown The rule for a reflection in the line y = x is ( x , y ) → ( y , x )7/7/ · Reflecting over y= x 0 How do you prove that the point P (x,y) becomes P' (y,x) after reflecting upon the line y=x?7/4/15 · Homework Statement Let T R 2 →R 2, be the matrix operator for reflection across the line L y = x a Find the standard matrix T by finding T(e1) and T(e2) b Find a nonzero vector x such that T(x) = x c Find a vector in the domain of T for which T(x,y) = (3,5) Homework Equations The Attempt at a Solution


Illustrative Mathematics



Ixl Reflections Find The Coordinates 7th Grade Math
4/12/ · Reflecting over the line y = x or y = x (the lines y = x or y = x as the lines of reflection) When you reflect a point across the line y = x, the xcoordinate and the ycoordinate change places When you reflect a point across the line y = x, the xcoordinate and the ycoordinate change places and are negated (the signs are changed)Reflection of a point across the line y = x The coordinate of point P is (1, 4) and the coordinate of the reflected image P' is (4, 1) The coordinate of point A is (5, 2) and the coordinate of the reflected image A' is (2, 5) Just swap the xcoordinate with the ycoordinate In general, when reflecting a point across the line y = x, if theThe linear transformation matrix for a reflection across the line $y = mx$ is $$\frac{1}{1 m^2}\begin{pmatrix}1m^2&2m\\2m&m^21\end{pmatrix} $$ My professor gave us the formula above with no explanation why it works



Movimientos En El Plano



Reflection Over The Line Y X Geogebra
For example, when reflecting the point (2,5) over y=xA reflection (or flip) is one kind of transformation The reflection of a point is another point on the other side of a line of symmetry Both the point and its reflection are the same distance from the line The following diagram show the coordinate rules for reflection over the xaxis, yaxis, the line y = x and the line y = xApply a reflection over the line x=3 Since the line of reflection is no longer the xaxis or the yaxis, we cannot simply negate the x or yvalues This is a different form of the transformation Let's work with point A first



Reflections Ck 12 Foundation



Reflection Definition Reflection In The Coordinate Plane
· What is the image of (0, 8) after a reflection over the line y = x?



Reflecting A Shape In Y X Using Cartesian Coordinates Key Stage 3
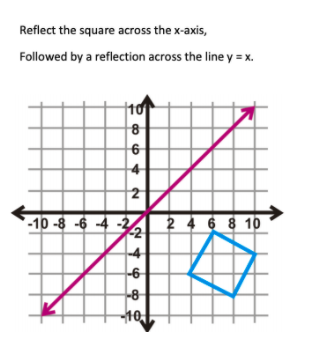


Solved Reflect The Square Across The X Axis Followed By Chegg Com
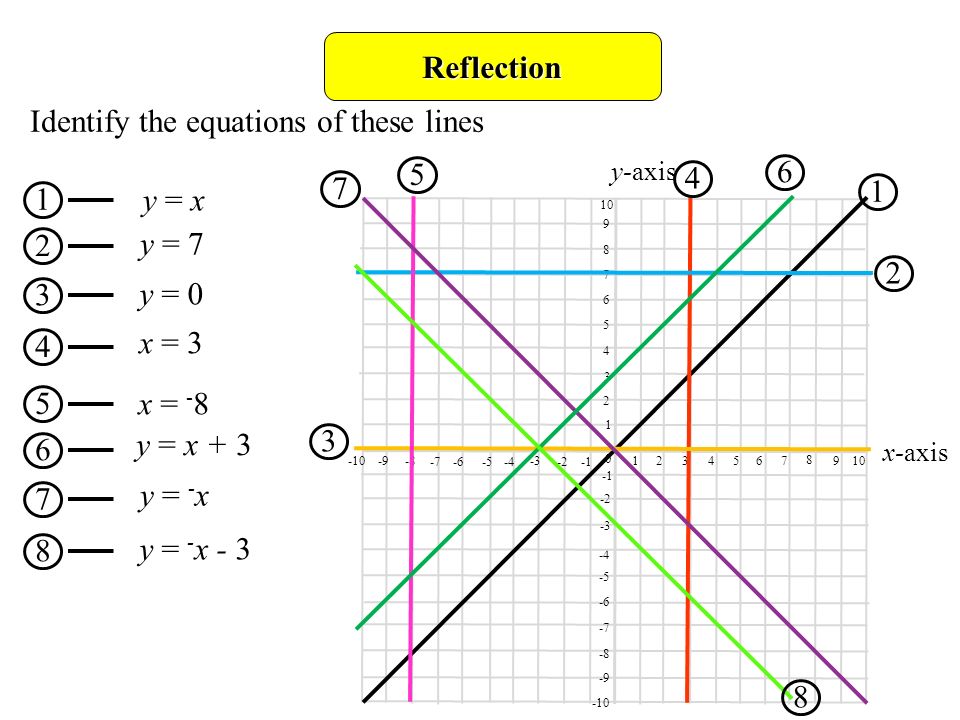


Reflection Objectives D Gradereflect Shapes In Lines Such As X 2 Or Y 1 Describe Reflections Fully Identify Reflection Symmetry In 3 D Solids Prior Ppt Download


1 Geometry Ms Singarajah 7



9 13 18 Reflections Geometry Blog



Reflection Mathbitsnotebook A1 Ccss Math



Solved Graph The Image Of The Polygon After A Reflection Chegg Com


Math Practice Problems Transformations 2



Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines


Transformation Matrix For Reflection In Y X Youtube


4 4 Transformations With Matrices 2 Reflections And
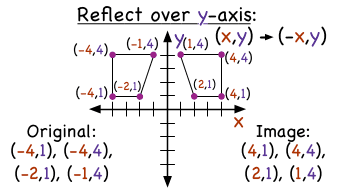


How Do You Use Coordinates To Reflect A Figure Over The Y Axis Virtual Nerd



Reflection Over The Line Yx Cute766



Reflections Ck 12 Foundation



Translation With Geogebra Figure 2 Reflection Through Line Y X With Download Scientific Diagram


Biomath Transformation Of Graphs


Untitled Document


Reflection Notes Videos Qa And Tests Grade 9 Optional Mathematics Transformation Kullabs


Warmup Reflect Triangle Abc Across The Line Y


Reflection Of A Point In A Line Assignment Point


Why Aren T Reflected Lines Perpendicular Meaning Why Are Their Slopes Negative Not Negative Reciprocals Enotes Com
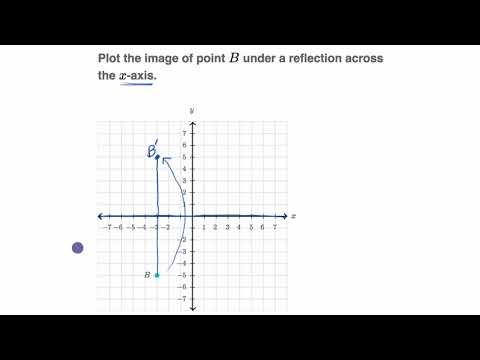


Reflecting Points Video Reflections Khan Academy
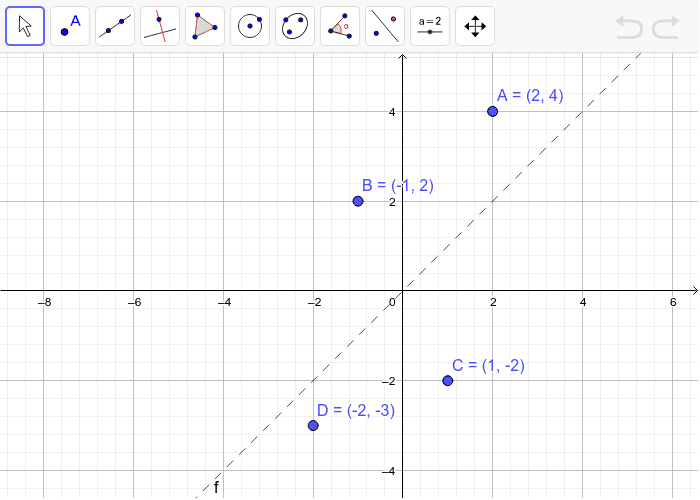


Reflecting In The Line Y X 2 Geogebra
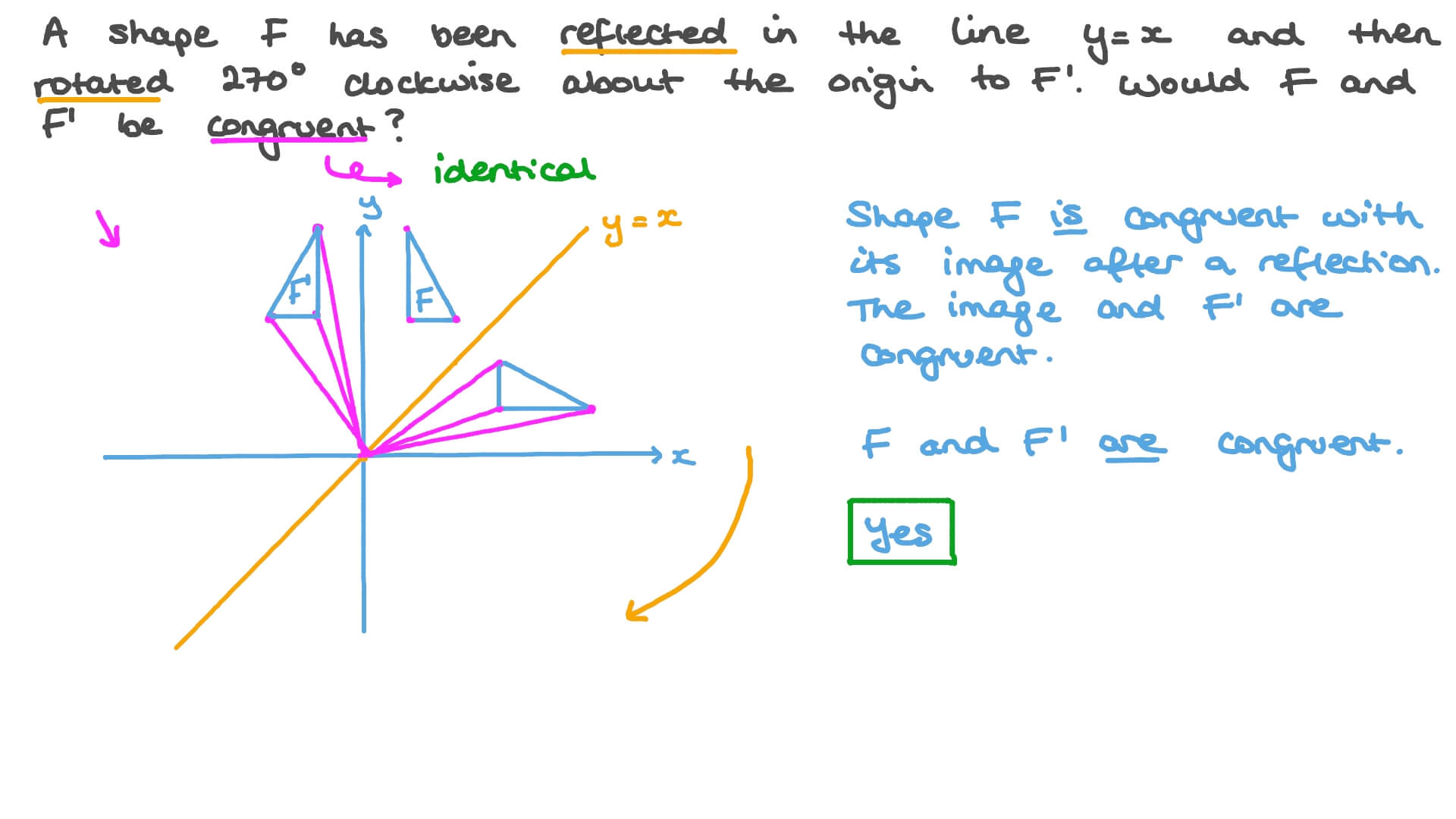


Question Video Understanding The Effects Of Reflection And Rotation On A Shape Nagwa
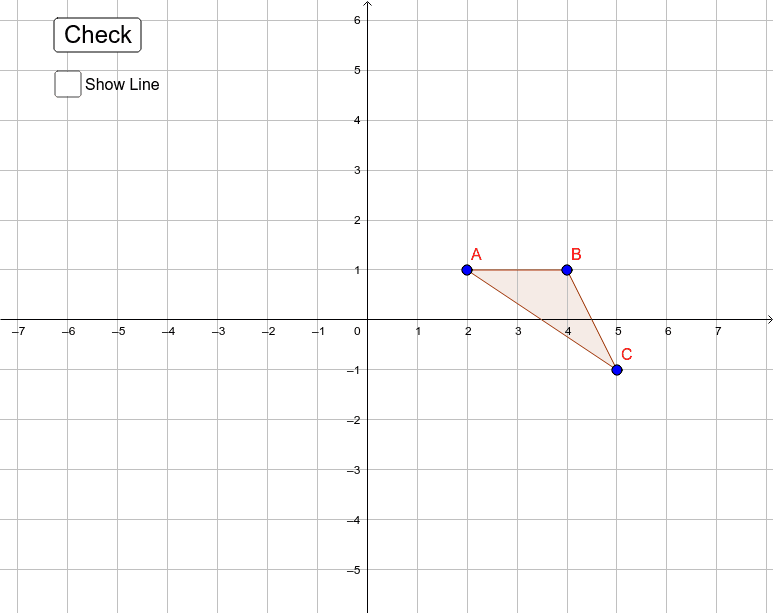


Reflection Over Y X Geogebra


Solution After A Reflection In The Line Y X 8 3 Is The Image Of Point Q What Is The Original Location Of Point Q



Reflection Mathbitsnotebook A1 Ccss Math


Solution After A Reflection In The Line Y X 2 4 Is The Image Of Point N What Is The Original Location Of Point N



Write The Coordinates Of The Vertices After A Reflection Across The Line Y X Brainly Com


What Does It Mean To Reflect Over The Y X Line Quora



Transformations



Transformations Boundless Algebra



Picture Of Reflection Across Y Axis Reflection Math Reflection Math



How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com



Reflections Geometry Abroad



Reflection In The Line Y X Geogebra



Solution What S The Result When We Reflect Y Sin X Twice Trigonometry Triangles To Functions Underground Mathematics



Reflection Mathbitsnotebook A1 Ccss Math



Transformation Reflection Over The Line Y X Youtube



Reflection Over The X And Y Axis The Complete Guide Mashup Math



Transformations Of Graphs


What Is The Image Of 2 5 Reflected Across X 2 Socratic
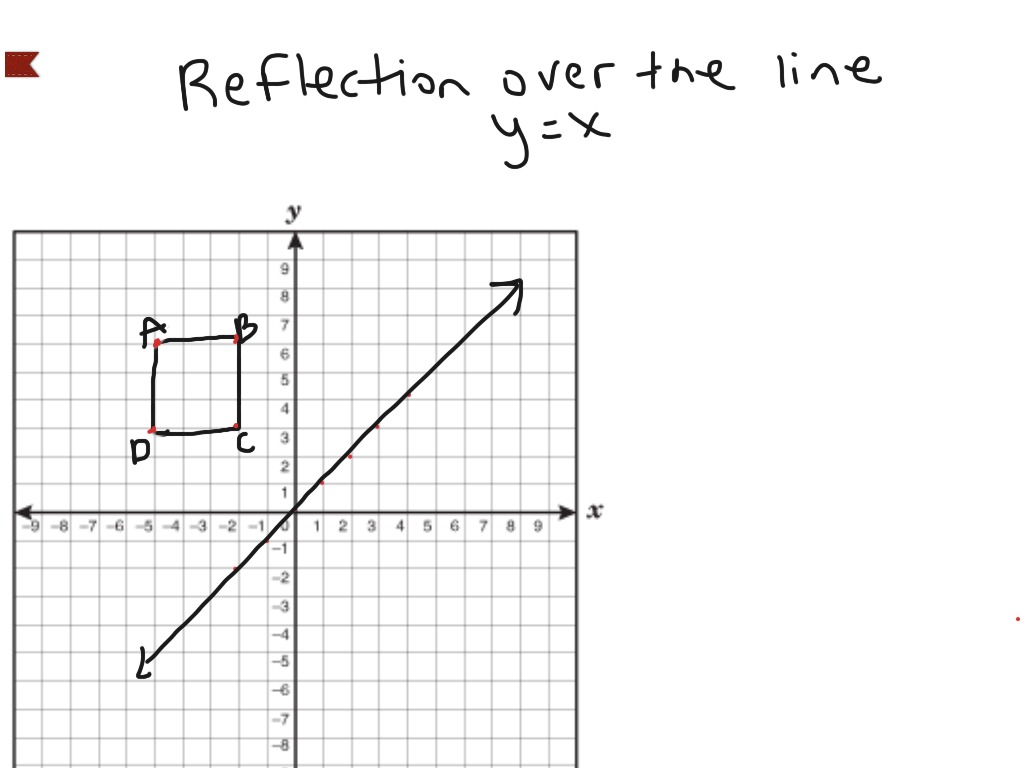


Reflection Over The Line Y X Math Showme



A Line Segment Goes From 1 2 To 4 1 The Line Segment Is Reflected Across X 1 Reflected Across Y 3 And Then Dilated About 2 2 By A Factor


Reflection



Reflection Over The Line Y X Youtube


Math Alive Geometry 1


Point 4 3 Is Reflected Over The Line Y X What Are The Coordinates Of The Reflection Mathskey Com
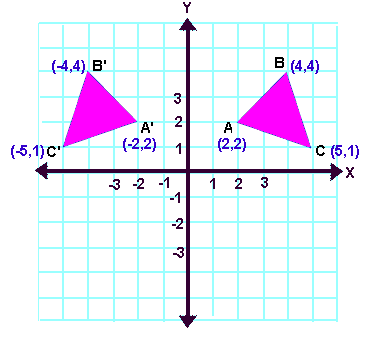


Reflection Transformation Matrix



What Is A Line Of Reflection Printable Summary Virtual Nerd



Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines



Reflection Over The Y X Line Youtube



Reflection Over Y X Math Geometry Showme


Solution The Line With The Equation Y 2x 3 Is Reflected In The Y Axis Find The Equation Of The Image Line



How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com
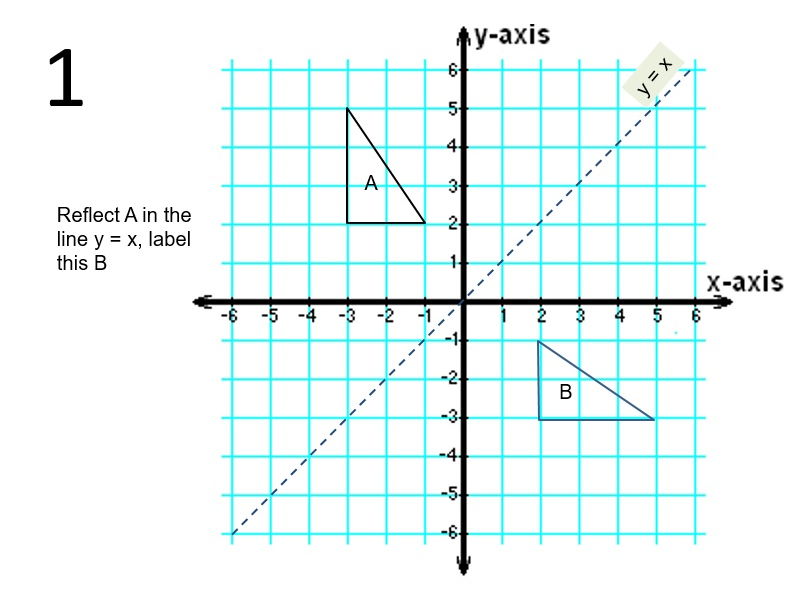


Diagonal Reflections In The Line Y X Teaching Resources



Kite Abcd Is Reflected Over The Line Y X What Rule Shows The Input And Output Of The Reflection Brainly Com



Reflection In Geometry Examples Solutions Videos Worksheets Games Activities
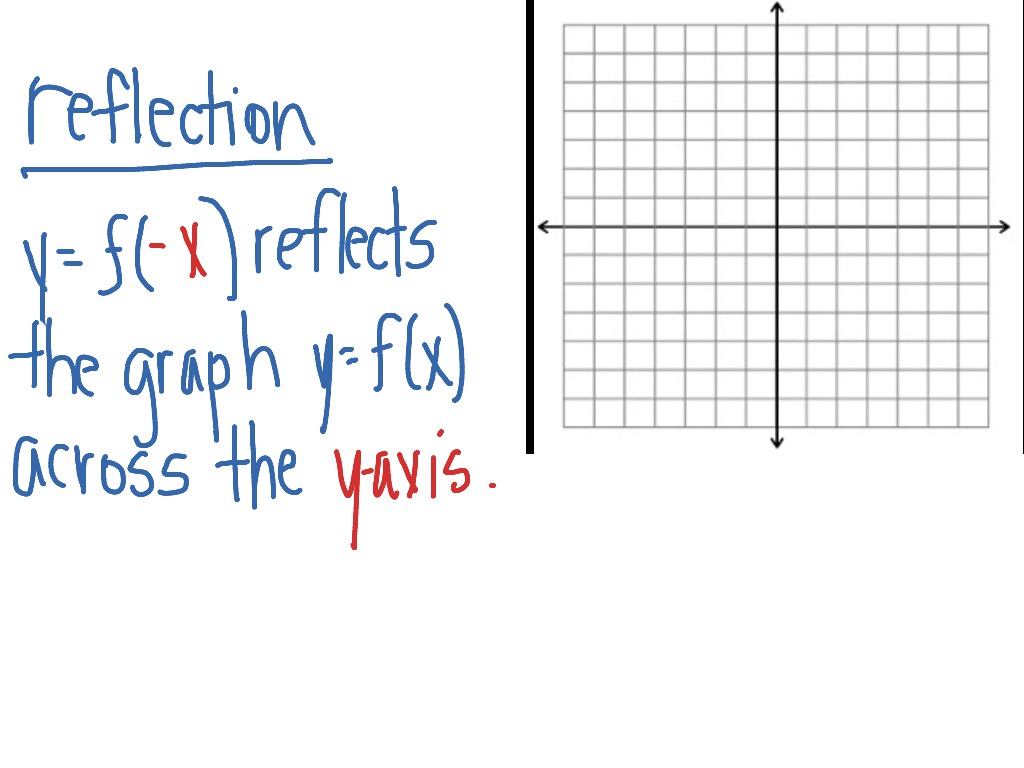


Reflection Across The Y Axis Math Functions Showme



Coordinate Geometry Reflections On A Coordinate Plane Magoosh Math



Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines



Reflection Over The Line Y X Math Showme



Picture Of Reflection In The Line Y X Reflection Math Math Reflection



Common Reflections Key Stage 3



How To Find A Reflection Image
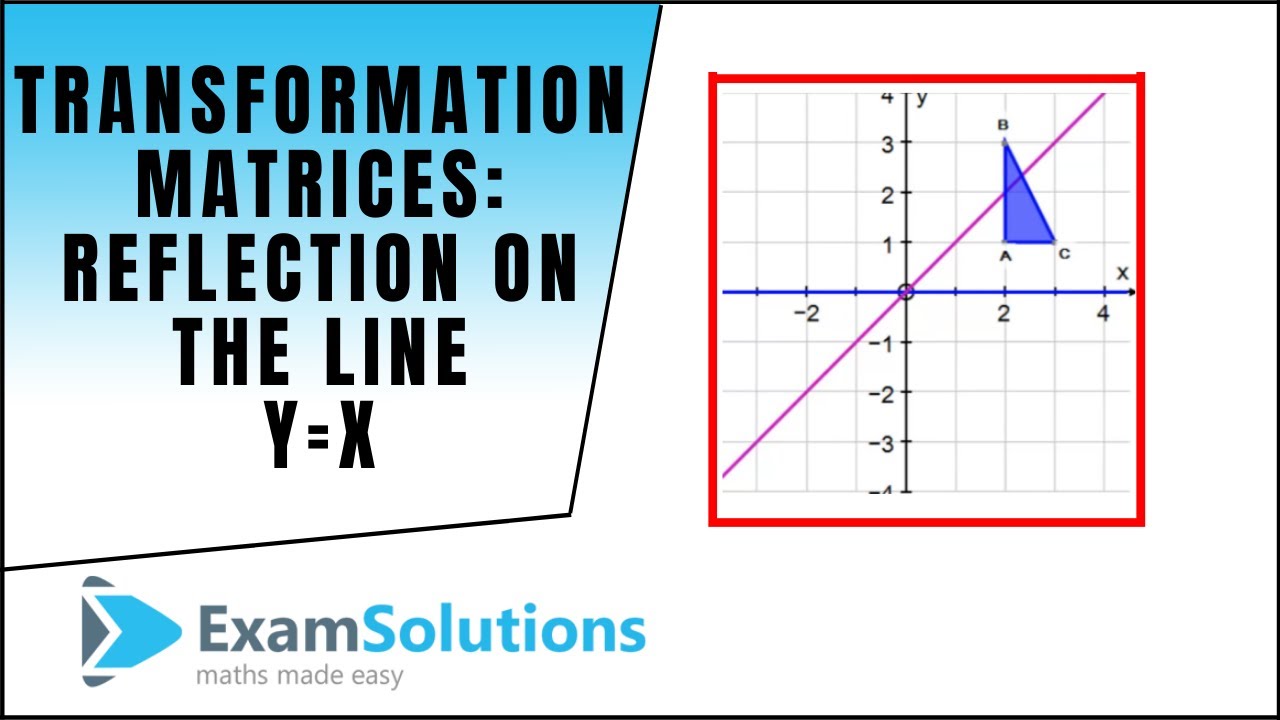


Transformation Matrices Reflection The Line Y X Examsolutions Maths Tutorials Youtube



Common Reflections Key Stage 3



Reflection Over A Line Expii



10 Math Problems Transformation Reflection



What Are The Coordinates Of Point A 4 1 After It Has Been Reflected Over The Y Axis Socratic



Reflections Through The Axes And The Lines Y X And Y X Geogebra



Reflection Mathbitsnotebook A1 Ccss Math



Learn About Reflection Over The Line Y X Caddell Prep Online



How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com



Reflection Over Y 2 With Rule Educreations



How To Reflect A Graph Through The X Axis Y Axis Or Origin



0 件のコメント:
コメントを投稿