Solution for 2xy=6 equation Simplifying 2x y = 6 Solving 2x y = 6 Solving for variable 'x' Move all terms containing x to the left, all other terms to the right Add '1y' to each side of the equation 2x y 1y = 6 1y Combine like terms y 1y = 0 2x 0 = 6 1y 2x = 6 1y Divide each side by '2' x = 3 05y Simplifying xGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutor
Maths Guru Please Help Me Solve This Simultaneous Equations For My Young Photo Education 2 Nigeria
2x+x-y/6=2 x-2x+y/3=1 by elimination method
2x+x-y/6=2 x-2x+y/3=1 by elimination method-The elimination method for solving systems of linear equations uses the addition property of equality You can add the same value to each side of an equation So if you have a system x – 6 = −6 and x y = 8, you can add x y to the left side of the first equation and add 8 to the right side of the equation And since x y = 8, you are adding the same value to each side of the first I Solve by elimination method 1 x2y1=0 and 2x 3y – 12 =0 2 2x – y = 6 and x – y = 2 3 X y = 3 and 2x5y=12 4 2x3y = 4 and xy 3=0 5 3x2y =12



How To Solve The Following Simultaneous Equations By Elimination Method A 2x 3y 12 X Y 1 B 3x Y 10 C X 3y 1 3x 2y 4 0 D 5 Quora
Solve by Addition/Elimination x2y=3 2x3y=9 x − 2y = 3 x 2 y = 3 2x − 3y = 9 2 x 3 y = 9 Multiply each equation by the value that makes the coefficients of x x opposite (−2)⋅ (x−2y) = (−2)(3) ( 2) ⋅ ( x 2 y) = ( 2) ( 3) 2x−3y = 9 2 x 3 y = 9 Simplify Tap for more steps Simplify ( − 2) ⋅ ( x − 2 yThe simultanous equation calculator helps you find the value of unknown varriables of a system of linear, quadratic, or nonlinear equations for 2, 3,4 or 5 unknowns A system of 3 linear equations with 3 unknowns x,y,z is a classic example This solve linear equation solver 3 unknowns helps you solve such systems systematicallySolve the system by the elimination method 2x y 6 = 0 2x y 8 = 0 When you eliminate x, what is the resulting equation?
Algebra Systems of Equations and Inequalities Linear Systems with Addition or Subtraction 1 Answer Dean R How do you use the addition and subtraction method to solve a linear system?2xy=6,2xy=2 To solve a pair of equations using substitution, first solve one of the equations for one of the variables Then substitute the result for that variable in the other equation 2xy=6 Choose one of the equations and solve it for x by isolating xLet's explore a few more methods for solving systems of equations let's say I have the equation 3x plus 4y is equal to 25 and I have another equation 5x 5x minus 4y is equal to twenty five point five and we want to find an x and y value that satisfies both of these equations if we think of it graphically this would be the intersection of the lines that represent the solution sets to both of
Multiply the both sides of the second equation by 2 Distribute and multiply Now add the equations together You can do this by simply adding the two left sides and the two right sides separately like this Group like terms Elimination Method Steps Step 1 Firstly, multiply both the given equations by some suitable nonzero constants to make the coefficients of any one of the variables (either x or y) numerically equal Step 2 After that, add or subtract one equation from the other in such a way that one variable gets eliminatedNow, if you get an equation in one variable, go to Step 3The method of elimination is a useful tool that will be used here in order to get the solution or a pair of values of x x and y y such that both the equations satisfy simultaneously In this




Solve X Y 3 And X 3 Y 2 6 By Substituting Methos Scholr




2x Y 6 0 4x 2y 4 0 Solve By Substitution Elimination And Graph Maths Pair Of Linear Equations In Two Variables Meritnation Com
2xy=6 Simple and best practice solution for 2xy=6 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve itMathematics To eliminate y, double the second equation and add it to the first 2(3x 2y) (2x 4y) Xyz=5 2y3z=14 3y2z=5 solve the system useing any algebraic method?Elimination method refers to the addition method of solving a set of linear equations This is quite similar to the method that you would have learned for solving simple linear equations Consider this example Consider a system x – 6 = −6 and x y = 8




Solve The Following System Of Equations 27 X Y 15 X Y 2 And 30 X Y 1 X Y 3 Mathematics Topperlearning Com X68shsoo



What Is X And Y When X Y 10 And X Y 6 Simultaneous Equation Quora
Ex 34, 1 (Elimination) Solve the following pair of linear equations by the elimination method and the substitution method (i) x y = 5 and 2x – 3y = 4 x y = 5 2x – 3y = 4 Multiplying equation (1) by 2 2(x y) = 2 × 5 2x 2y = 10 SolvingClick here👆to get an answer to your question ️ Solve the following pairs of linear equation by the elimination method and the substitution method(i) 3x 5y 4 = 0 and 9x = 2y 7 (ii) x2 2y3 =Textbook solution for College Algebra 10th Edition Ron Larson Chapter 62 Problem 13E We have stepbystep solutions for your textbooks written by Bartleby experts!



A B 8 X Y 6 A X 13 And B Y 8 What Is The Value Of A B X And Y Quora



The Substitution Method
For Solving Pair of Equation, in this Exercise Use the Method of Elimination by Equating Coefficients X Y /6 = 2( 4 X ) 2x Y = 3( X 4 ) CISCE ICSE Class 9 Question Papers 10 Textbook Solutions Important Solutions 5 Question Bank Solutions Concept Notes Solve by eliminnation methods 2x4y=5 2x4y=6 solve the system by elimination method 5x2y= 13 7x3y=17 Solve x64 Determine whether the given numbers are solutions of the inequality 8,10,18,3 y8>2y3 Solve by theVisit http//ilectureonlinecom for more math and science lectures!In this lecture series I'll show you how to solve for multiple variables simultaneously us




X 3y 6 0 2x Y 5 By Elimination Method Brainly In




X Y 2xy X Y Xy 6 By Elimination Method Brainly In
Solve the system by the elimination method 2x 3y 10 = 0 4x 3y 2 = 0 1 See answer luticiawright is waiting for your help Add your answer and earn pointsFree system of equations calculator solve system of equations stepbystepSolve the system by the elimination method 2x y 6 = 0 2x y 8 = 0 When you eliminate x, the resulting equation is 2y = 22x y 6 2x y 8 = 0;



Solved Find The Common Solution Of Each Using The Elimination And Substitution Method 2x Y 2 X 3y 36 B Course Hero
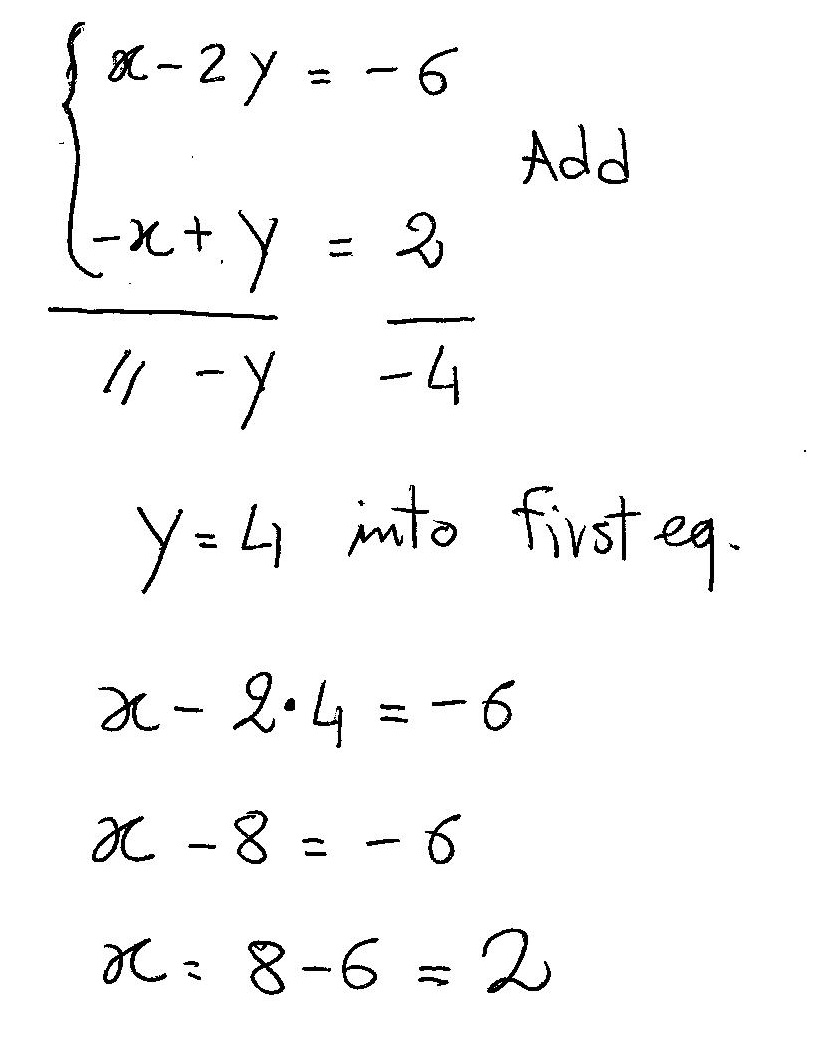



How Do You Solve X 2y 6 And X Y 2 Socratic
Solve the system by the elimination method 3x 2y 7 = 0 5x y 3 = 0 To eliminate y, the LCM is 2 Which of the following is the resulting equations?2y = 2 2y = 2 y = 2 1 See answer wandawhite455 is waiting for your help Add your answer and earn pointsQuestion Solve using the elimination method x y = 6, x 3y = 2 Answer by stanbon(757) (Show Source) You can put this solution on YOUR website!



Make A Table Of Solutions And Graph The Equation X Y 6 Mathskey Com



Link Springer Com Content Pdf m 3a978 1 349 3 2f1 Pdf
Solve using the elimination method x y = 6, x 3y = 2Add the two equations to get 4y = 4 y = 1Substitute into xy=6 to solve for "x" x 1 = 6 x = 5Click here👆to get an answer to your question ️ Solve the following by elimination method 2x y = 6 and x 2y = 2Gaussian Elimination means that the augmented matrix should be reduced to a triangular matrix, and then How To Solve Equation By Elimination 2x4y=4 3x2y=18?



Solve The Following Systems Of Equations X Y Xy 2 X Y Xy 6 Sarthaks Econnect Largest Online Education Community



Solve The Following Systems Of Equations Graphically X Y 6 X Y 2 Sarthaks Econnect Largest Online Education Community
Solve using the elimination method Show your work If the system has no solution or an infinite number of solutions, state this 2x 6y = 12 x 3y = 3 3 Solve using the elimination method Show read more New answers Rating 8 yeswey x 3y = 0 (equation 1) 3y 6 = 2x rearranging the equation in standard form 2x 3y = 6 (equation 2) adding up equation 1 and 2 the result is;2xy6=0, 4x2y4=0 solve by substitution, elimination And graph Maths Pair of Linear Equations in Two Variables



The Substitution Method




Ex 3 4 1 Solve By Elimination And Substitution I X Y 5 2x 3y
1 seconds Q Which method would be best (quickest) for solving the system below 3x 4y = 2 y = 2x 1 answer choices Substitution Elimination GraphingSolve for substitution and elimination x2y=9 and 2x5y=33 show your work asked in ALGEBRA 2 by angel12 Scholar systemofequations;About Elimination Use elimination when you are solving a system of equations and you can quickly eliminate one variable by adding or subtracting your equations together You can use this Elimination Calculator to practice solving systems
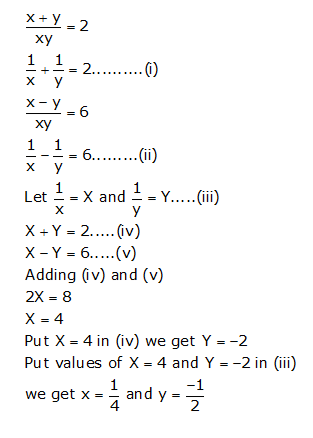



Solve The Following System Of Linear Equations X Y 2 X Y 6 Xy Xy Mathematics Topperlearning Com D9jn35dd




2x Y 6 X Y 2 By Cross Multiplication Method Brainly In
Solving Linear Equations by Elimination Method Here we are going to see some example problems of solving linear equations in two variables using elimination method The various steps involved in the technique are given below Step 1 Multiply one or both of the equations by a suitable number (s) so that either the coefficients of firstPlay this game to review Mathematics Solve using Elimination Method x y = 11 2x y = 19How Do You Solve a System of Equations Using the Elimination by Multiplication Method?




Solve The Following Pair Of Linear Equation By Substitution Method 3x 2y 7 0 4x Y 6 0




Graph Graph Inequalities With Step By Step Math Problem Solver
Answer to Solve the system of equations using the elimination method 2x 3y = 2 4x y = 6 By signing up, you'll get thousands of stepbystep Solve xy=1 and 2xy=8 by elimination method simplify √16√4√36the answer will be marked as brilliant in 10 minutesSOLUTION using elimination method solve problem 3x2y=1 4xy=6 You can put this solution on YOUR website!




Ex 3 4 1 Solve By Elimination And Substitution I X Y 5 2x 3y



If X Y 3 X Y 1 Then What Is X Y Quora
2y = 2 THIS SET IS OFTEN IN FOLDERS WITHSolve for x and y using elimination method xy/xy=2 xy/xy=6 Hi, you may find many different solutions but this is the simplest but check the answer firstFind the solution to the following system of equations 4x – 2y = 4 and 2x y = 6




Graph Graph Inequalities With Step By Step Math Problem Solver




Ex 3 6 1 V And Vi 7x 2y Xy 5 8x 7y Xy 15
3x 2y 7 = 0 Solve the system by the elimination method2x y 6 = 0 2x y 8 = 0 When you eliminate x, what is the resulting equation?The elimination method of solving systems of equations is also called the addition method To solve a system of equations by elimination we transform the system such that one variable "cancels out" Example 1 Solve the system of equations by elimination $$ \begin{aligned} 3x y &= 5 \\ x y &= 3 \end{aligned} $$Solution Step 1 Select a variable which you want to eliminate from the equations Let us select y y 4x−3y = 32 xy = 1 4 x − 3 y = 32 x y = 1 Step 2 Take suitable constants and multiply them with the given equations so as to make the coefficients of



How To Solve The Following Simultaneous Equations By Elimination Method A 2x 3y 12 X Y 1 B 3x Y 10 C X 3y 1 3x 2y 4 0 D 5 Quora
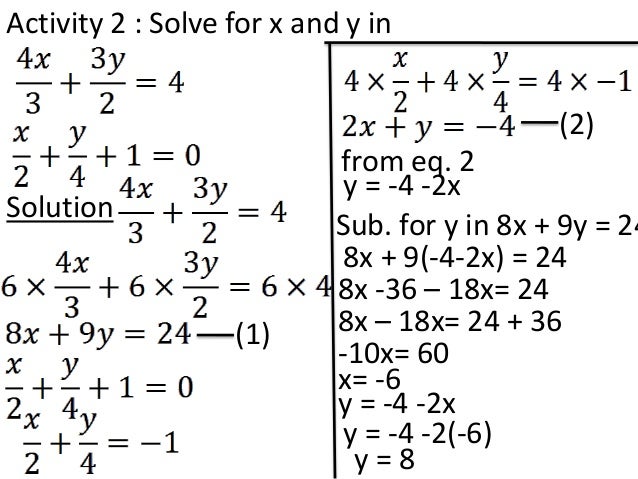



Simultaneous Equations
Step by step solution of a set of 2, 3 or 4 Linear Equations using the Substitution Method y=2x6;3xy=6 Tiger Algebra Solver The two lines have the same slope, therefore they are parallel and there is no solution Solve the system of equations Equation 1 y=2x6 Equation 2 2xy=2 If Equation 2 is converted from standard form to slopeintercept form, you will see that both lines have the same slope, and are therefore parallel lines, and there is no solutionSolve the system using method of elimination x' = x 2y y' = x y with the initial conditions x(0) = y(0) = 1 Get more help from Chegg Solve it with our calculus problem solver and calculator
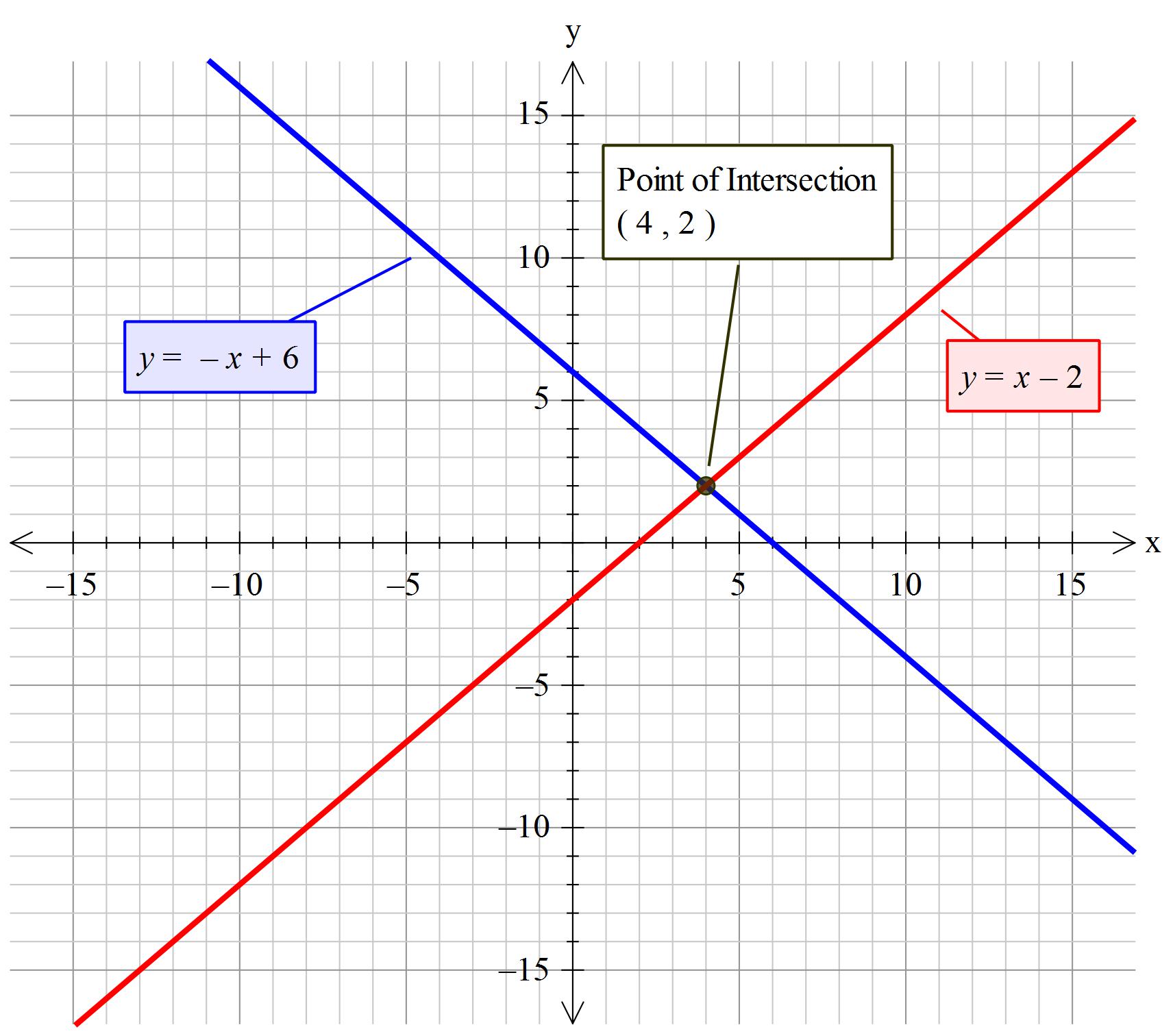



How Do You Solve The System X Y 6 And X Y 2 By Graphing Socratic



Make A Table Of Solutions And Graph The Equation X Y 6 Mathskey Com
How do you solve by elimination #x y = 2# and #2x y = 1#?X/2 2y/3 = 1 and xy/3=3 Find x and y values using Elimination and Substitution method(a) 2x 3y = 12(i) and x y = 1(ii) (ii)×3 ==> 3x 3y = 3(iii) Now we can eliminate y by adding (i) & (iii) (i) (iii) ==> 5x = 15 so x=3
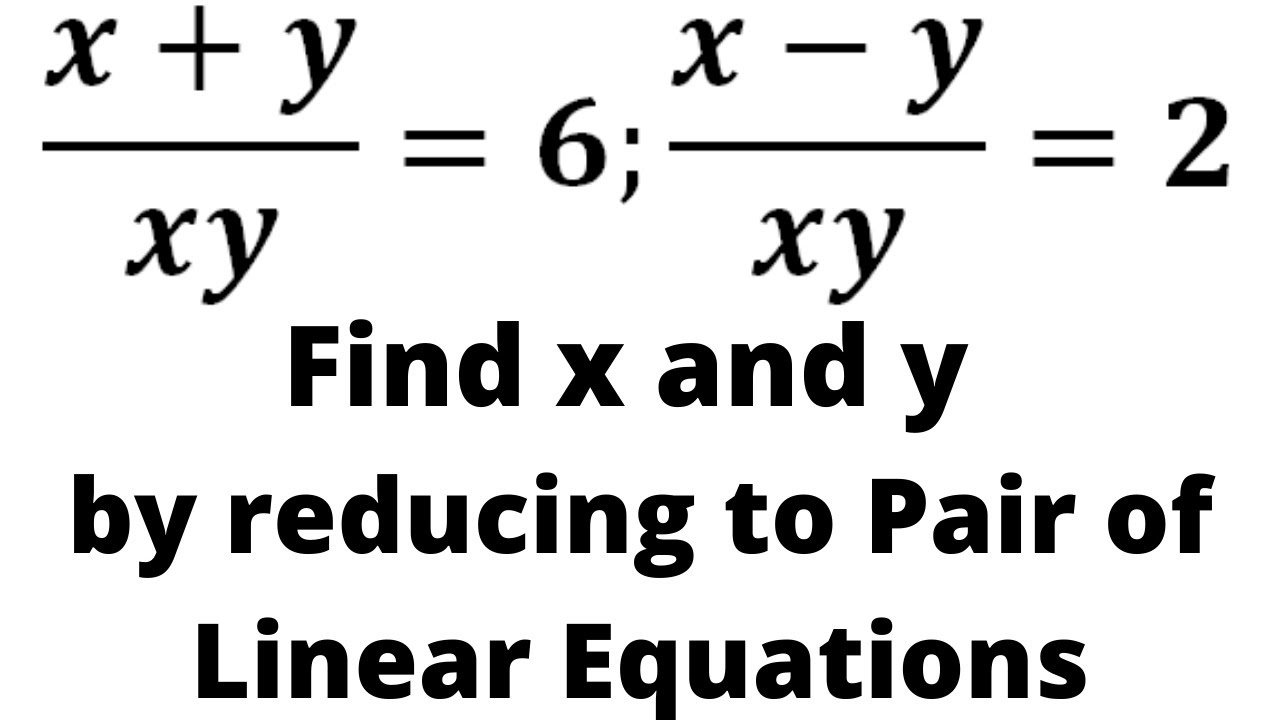



X Y Xy 6 X Y Xy 2 Find X And Y By Reducing Them To Pair Of Linear Equations Youtube




Solve The Equation 2x Y 6 0 And 2x Y 2 0 By Substitution Method Brainly In



Maths Guru Please Help Me Solve This Simultaneous Equations For My Young Photo Education 2 Nigeria




Ex 3 3 1 Solve By Substitution Method I X Y 14 Ex 3 3




Rd Sharma Solutions For Class 10 Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 4 Avail Pdf




Solve The Following System Of Equations By Method Of Cross Mult



Simultaneous Equations



How Do You Solve The System 2 X 4 Y 6 3x 2 Y 3 13 Socratic




R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 4



Solve The Following Systems Of Equations X Y 2xy X Y Xy 6 X 0 Y 0 Sarthaks Econnect Largest Online Education Community
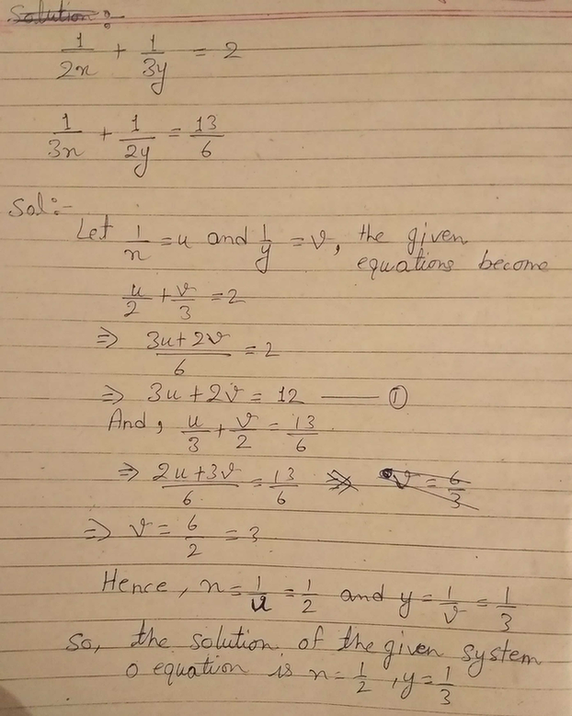



Exercise 3 5 1 Solve The Following Pairs Of Equations By Re Scholr



How To Solve For X And Y In X Y 5 And Xy 6 Quora



Solve The Following Systems Of Equations 6 X Y 7 X Y 3 1 2 X Y 1 A X Y Where X Y 0 And X Y 0 Sarthaks Econnect Largest Online Education Community




Solve Each Other Pair Of Equa See How To Solve It At Qanda
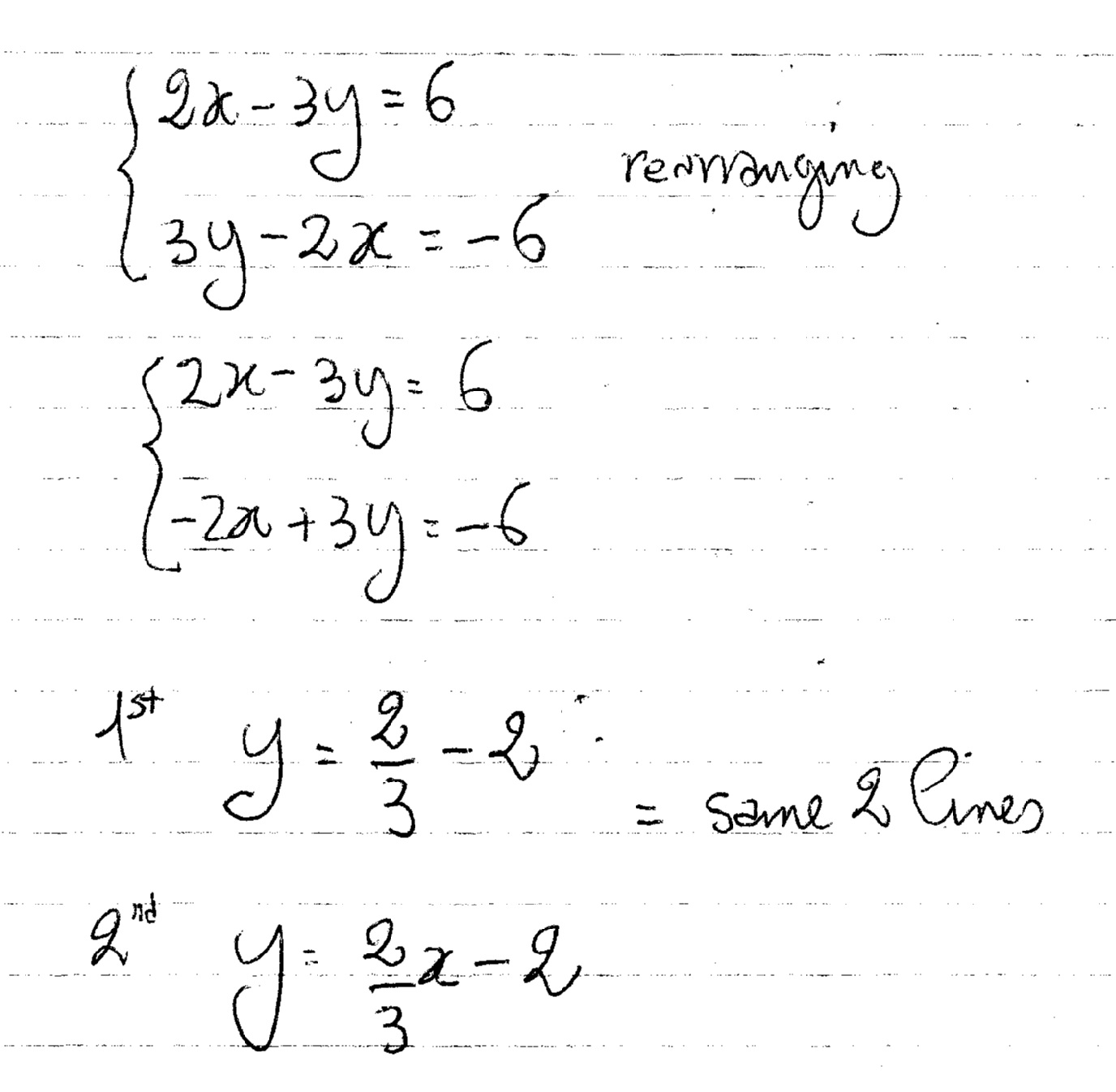



How Do You Solve The System Of Equations 2x 3y 6 And 3y 2x 6 Socratic



Math Storyboard Par F4529c
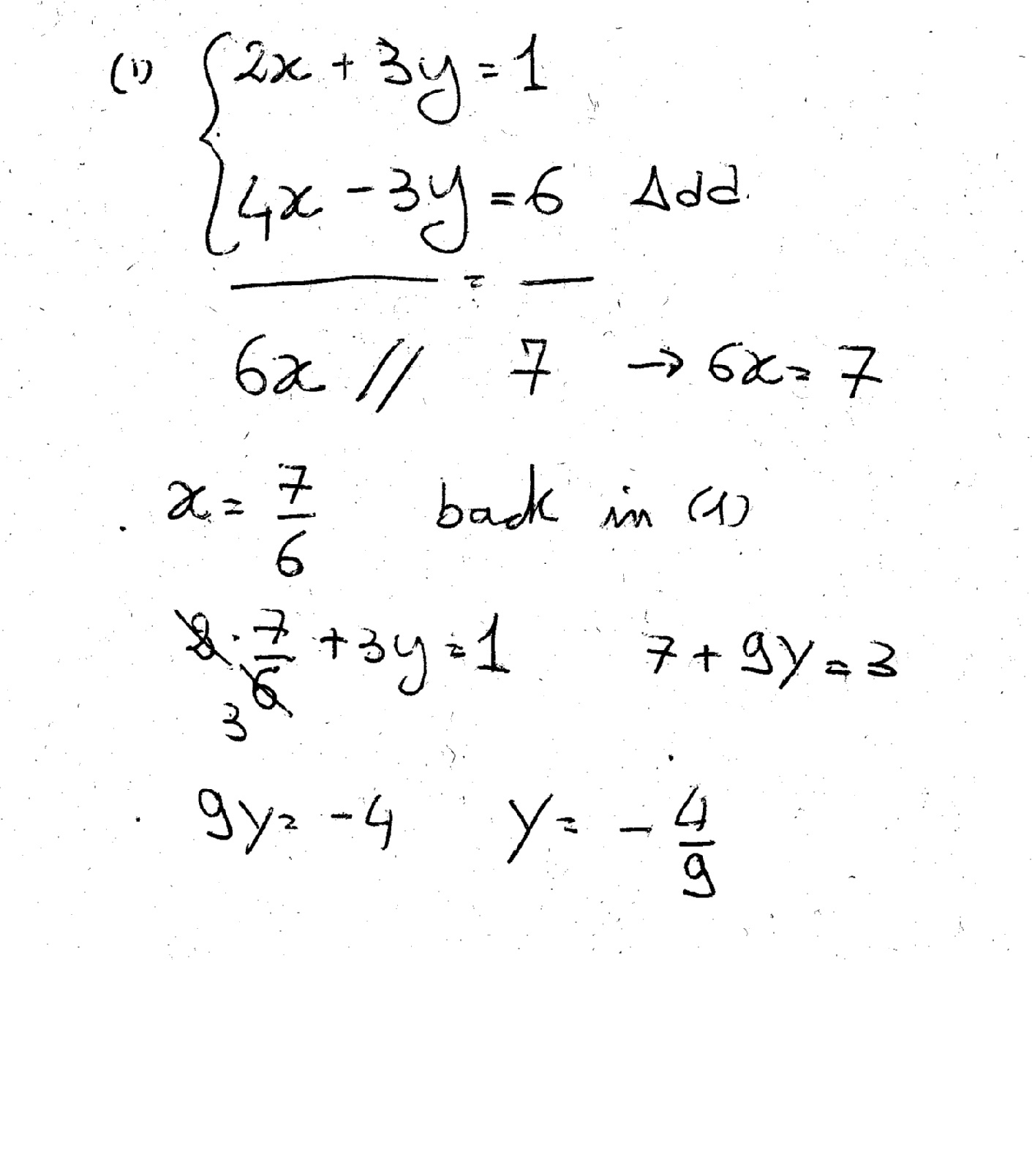



How Do You Solve The System Using The Elimination Method For 2x 3y 1 And 4x 3y 6 Socratic




X Y 6 X Y 2 Find Out Value Of X And Y Brainly In




Systems Of Equations Elimination Part Ii Unit 7 Lesson 5b Ppt Download



1




Solve The System X Y Z 6 X Y Z 2 2x Y Z 1 Using Matrix Inverse Youtube




Graphically Solve The Following Pair Of Equations 2x Y 6 And 2x Y 2 0 Find The Ratio Of The Areas Youtube




X Y 6 X Y 2 Find X And Y Brainly In




2x Y 6 X Y 2 By Elimination Method Brainly In




6 X Y 7 X Y 3 1 2 X Y 1 3 X Y



1




1 X Y 4 Practice Set 1 2 Complete The Following Table To Draw Graph Of The Equation 1 X Y 3 Ii X Y 4 X



How Do You Solve The System 2 X 4 Y 6 3x 2 Y 3 13 Socratic



6 2 Solving Systems Of Equations Using Elimination




Solve 2x Y 6 And 2x Y 2 0 By Elimination Method Brainly In



What Are X And Y From The System Equation 2x 3y 4 X Y 6 Quora



Solved Find The Common Solution Of Each Using The Elimination Substitution And Graphical Method 2x Y 2 X 3y 36 2 3x Y 6 X Y 6 3 Course Hero



Simultaneous Equations Gmat Math Study Guide



The Elimination Method




4 3 Systems Of Linear Equations In Three Variables




2 X Y 3 X Y 1 8 X Y 7 X Y 5 6 Solve X And Y Youtube




Solving Simultaneous Equations Equations And Inequalities Siyavula




X Y 2xy X Y 6xy Solve By Substitution Method Maths Pair Of Linear Equations In Two Variables Meritnation Com




Solve X Y 2x Y 6 2x Y 2 By Elimination Method Maths Pair Of Linear Equations In Two Variables Meritnation Com
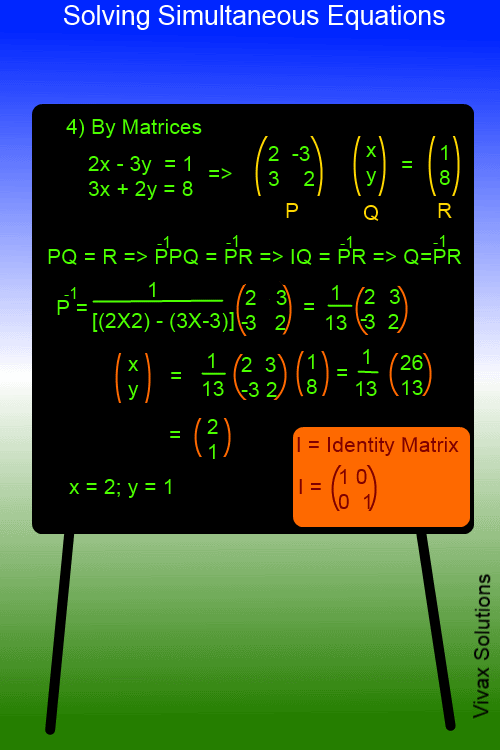



Solving Simultaneous Equations Elimination Substitution Graphical Matrix Methods Maths Tutorials Vivax Solutions




If X Y 6 And 3x Y 4 Then What Is X Y Equal To Quora
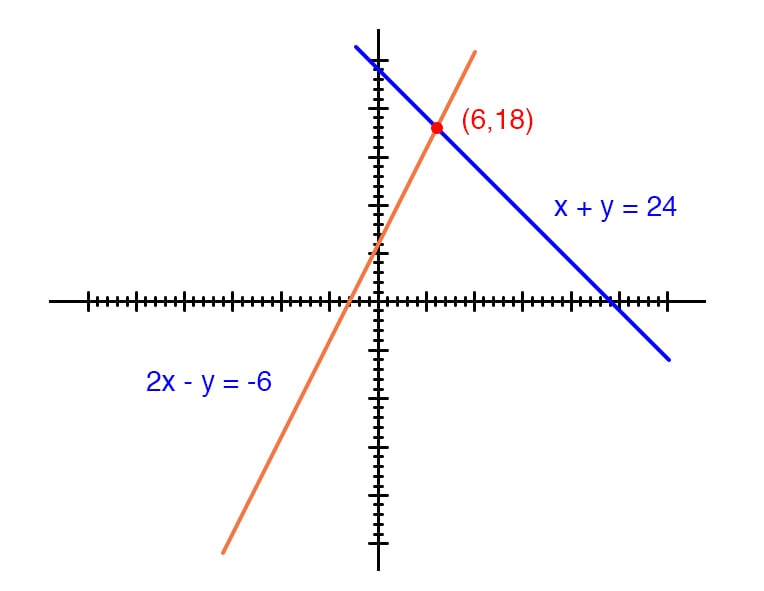



Solving Simultaneous Equations The Substitution Method And The Addition Method Algebra Reference Electronics Textbook




Solving Simultaneous Equations Equations And Inequalities Siyavula




Solve For X And Y 2x Y 6 And X Y 2 Brainly In




Do Now Solve Each System Using Elimination 2x 3y 8 X Y 2 Ppt Video Online Download
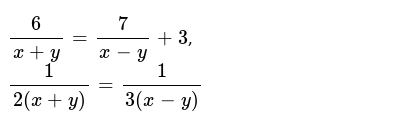



6 X Y 7 X Y 3 1 2 X Y 1 3 X Y




5 1 Exercises 9




Solve By Elimination Method X Y 6 X Y 4 Maths Linear Equations In Two Variables Meritnation Com




Urgent 10 X Y 2 X Y 4 15 X Y 5 X Y 2 Solve By Elimination Method Maths Pair Of Linear Equations In Two Variables Meritnation Com
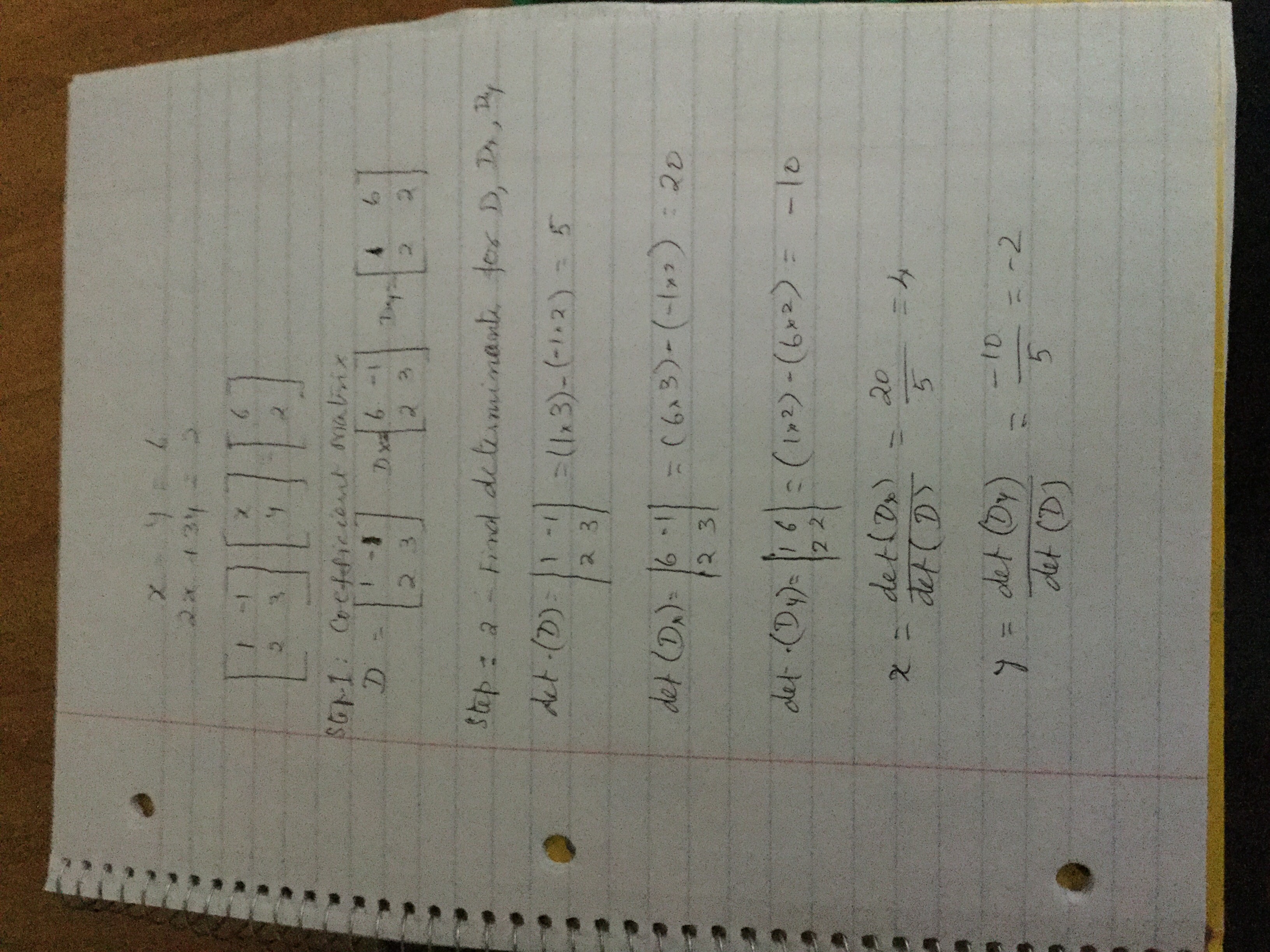



How Do You Solve X Y 6 And 2x 3y 2 Using Matrices Socratic




Solve The Following System Of Equations By Using Matrix Inversion Method 2x Y 3z 9 X Y Z 6 X Y Z 2




2x X Y 6 2 X 2x Y 3 1 Mathematics Topperlearning Com Fqktm544



1




Solve The Following System Of Equations By Method Of Cross Mult



10 X Y 2 X Y 4 And 15 X Y 5 X Y 2 P S 1 4 Q2 Linear Equation In Two Variables Youtube



How To Solve Using The Gauss Elimination Method Y Z 2 2x 3z 5 X Y Z 3 Quora



How To Graph Y 6 2x With Given Scale And Domain Youtube



Solve The Following Systems Of Equations X Y Xy 2 X Y Xy 6 Sarthaks Econnect Largest Online Education Community




Solve X Y 14 X Y 2




X Y Xy 2 And X Y Xy 6 By Elimination Method Brainly In



16 X Y 2 X Y 1 8 X Y 12 X Y 7 Find The Value Of X And Y Quora
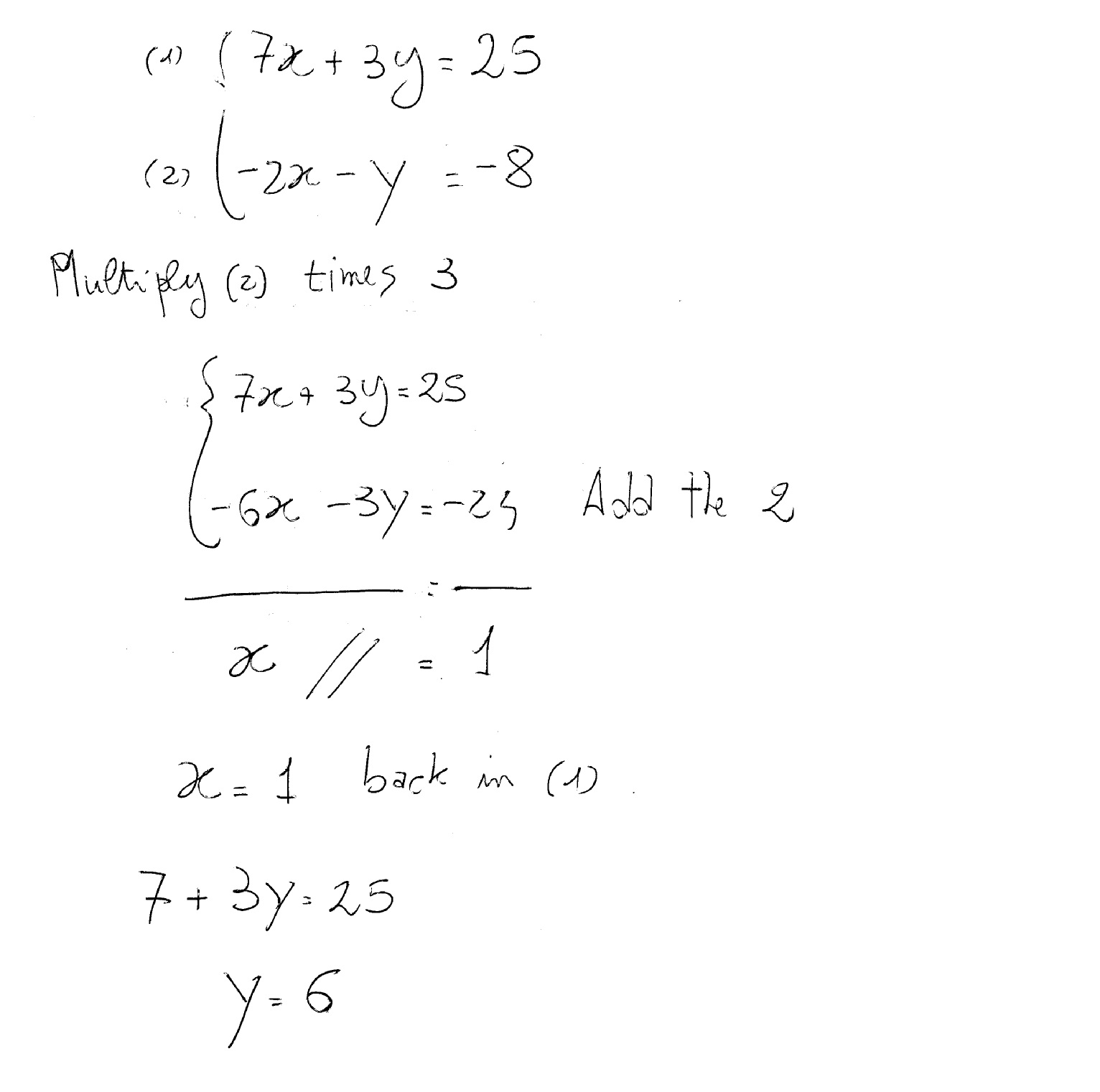



How Do You Solve The System 7x 3y 25 And 2x Y 8 Socratic




Solve For X And Y 40 X Y 2 X Y 5 And 25 X Y 3 X Y 1 Mathematics Topperlearning Com Idbi1itt




Solve The Following System Of Equations By Method Of Cross Mult




Systems Of Equations With Substitution Y 5x 8 10x 2y 2 Video Khan Academy




R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 4




X Y 3 X 3 Y 2 6 Youtube
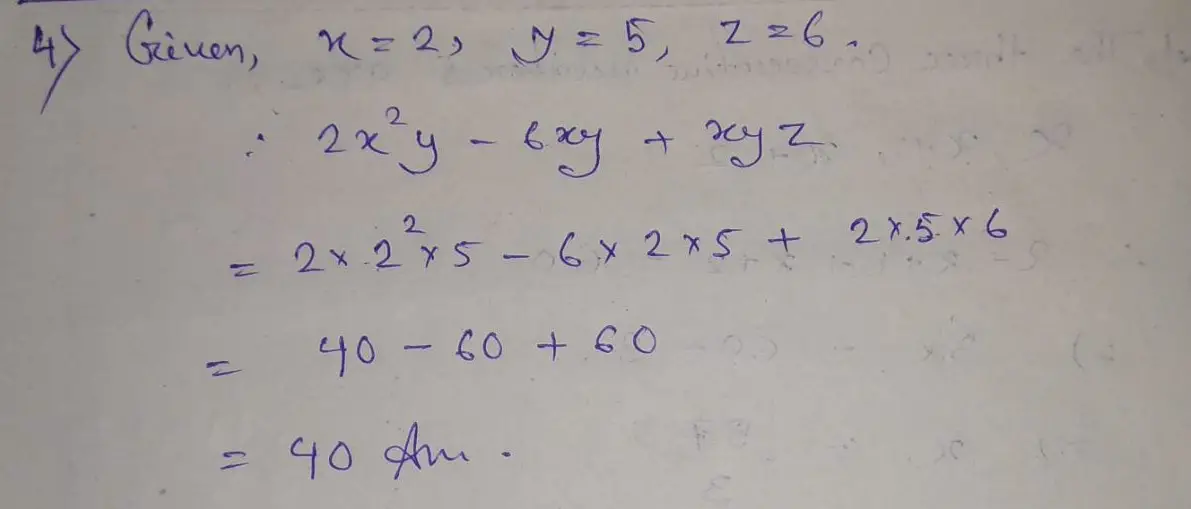



Algebra Extra Questions Solution For Class 6 Cbse Ncert Board Students




R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 3




6 2 Solving Systems Of Linear Equations 455 We Have Chegg Com




5 41 5 0 6 30 Solve Each System Using Gaussian Chegg Com
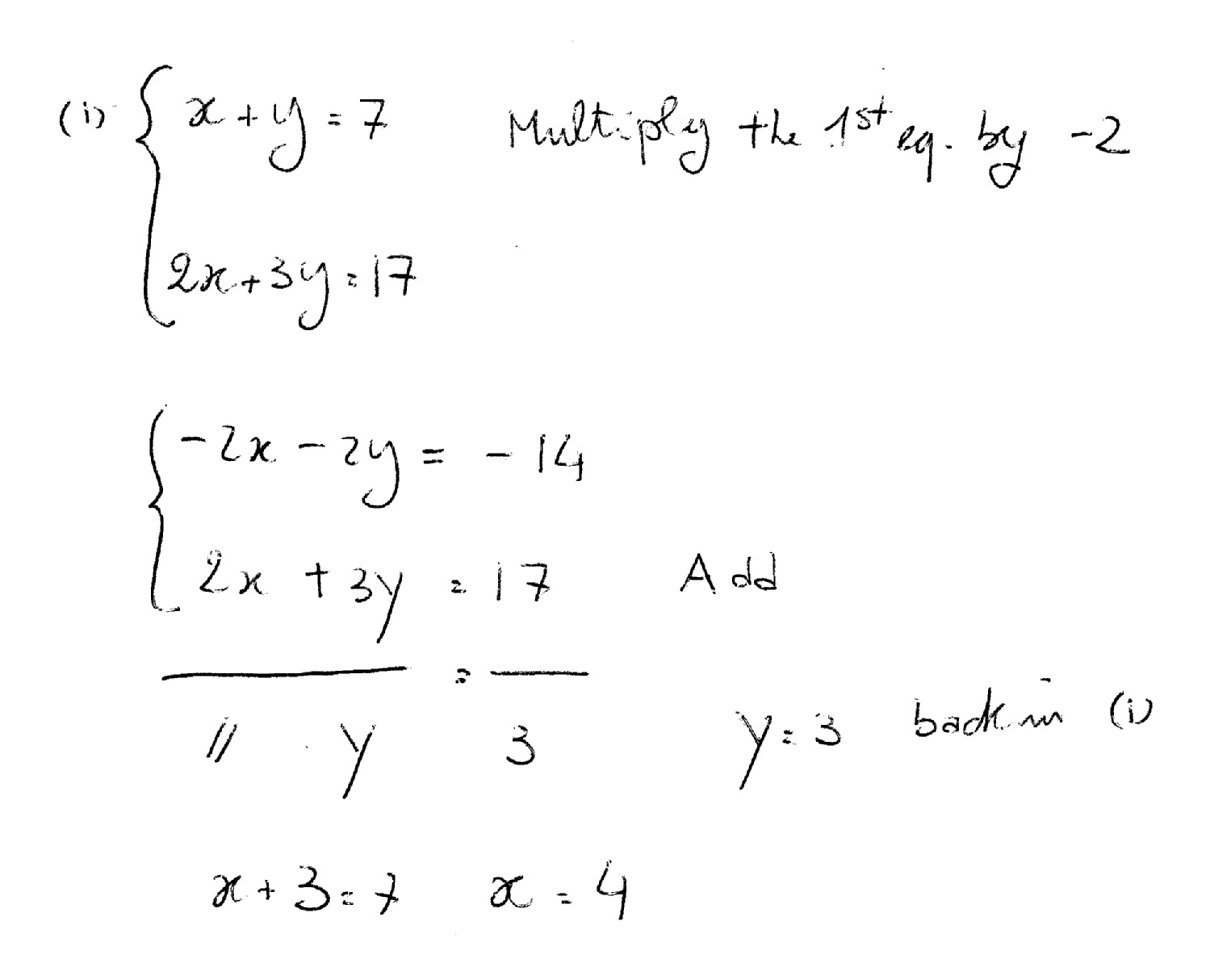



How Do You Solve The System Using The Elimination Method For X Y 7 And 2x 3y 17 Socratic



1
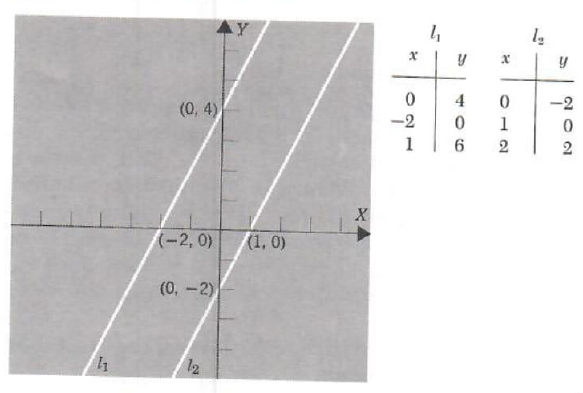



Solve System Of Equations Step By Step Math Problem Solver




X 3y 6 0 2x Y 5 Solve By Elimination Method Brainly In




Solving Simultaneous Equations Equations And Inequalities Siyavula



0 件のコメント:
コメントを投稿